Question 870286: Please help me solve this equation!
(a)Solve approximately the equations:
(i)2 sin x + cos x = 1.5
(ii)2 sin x + cos x = 0
(b)(i)3 cos x - 4 sin x + 1 = 0
(ii) 3 cos x = 4 sin x
PLEASE REPLY ASAP!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am learning something important from this problem (and from the wiki I found once I figured out how to ask the question).
Two of your problems (aii and bii) were easy to answer without much algebra and/or trigonometry.
The other two were clearly related, but required more algebra work.
There had to be a common strategy to solve all four problems,
and using trigonometric identities had to be the key,
but I could not see how to use trigonometric identities to get where I wanted to get.
A quick internet search led me to the common strategy to solve the problems.
EACH PROBLEM AS A SEPARATE STRUGGLE:
(a)(ii)
 <---> <---> <---> <---> <---> <--->
From there we know that  (in radians, or (in radians, or 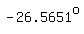 in degrees) is an answer. in degrees) is an answer.
Of course we know that there are infinite answers,  (in radians) apart from each other, (in radians) apart from each other,
because  is a periodic function with a period of is a periodic function with a period of  (with (with  expressed in radians). expressed in radians).
We could say that all of our approximate answers can be expressed as
 (with (with  and and  measured in radians). measured in radians).
The same strategy can be used to solve (b)(ii).
(I found  as a general solution). as a general solution).
(a)(i)
 <--> <--> --> --> <--> <-->
Calling  we can re-write the equation above as we can re-write the equation above as
 <--> <-->
We solve for  using the quadratic formula: using the quadratic formula:

The approximate solutions are

and  . .
With those values of  we set out to find we set out to find  . .
For  : :
There are two values of  between 0 and between 0 and  (or between (or between  and and  that yield that yield  . .
One is in quadrant I and the other in quadrant II.
With  , ,
to get  we need to have we need to have 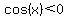 , ,
so we are looking foir a quadrant II solution.
 (in radians, or (in radians, or  in degress) is a solution. in degress) is a solution.
Another possible value is  (in radians, (in radians, 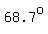 ) ), ) ),
but that is in quadrant I, with a positive  , and , and

does not satisfy  . .
For  : :
The solution  (in radians, or (in radians, or  in degrees), in quadrant I, with in degrees), in quadrant I, with 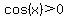 looks promising, looks promising,
as  can be can be  . .
In fact, it can be verified to satisfy  . .
On the other hand,  , in quadrant II, while it also yields , in quadrant II, while it also yields  , ,
it yields  and does not satisfy and does not satisfy  . .
The solutions highlighted above, are the solutions between 0 and  , ,
and in general, all solutions can be expressed as
 or or 
(with  and and  measured in radians). measured in radians).
The same strategy can be used to solve (b)(i).
(The general solutions I found are
 or or  ). ).
A COMMON STRATEGY:
The left side of the equation in (a)(ii) is

It is a "linear combination of sine and cosine functions".
That is a periodic function, like sine and cosine.
I can see that its period is  . .
It must be possible to express it as a single trigonometric function,
maybe  ,with two constants ,with two constants  and and  , ,
where the cosine function is shifted right by  and dilated vertically by a factor and dilated vertically by a factor  . .
Now, how could I use trigonometric identities to transform
 and and 
into a function like  ? ?
It required a lot of thinking, and on the Sunday morning after such a Saturday night, I did not trust my brain that much.
I just googled "linear combinations of sine and cosine functions",
and helped myself to someone else's thinking.
Trigonometric identities tell us that

so 
So if a linear combination of sine and cosine functions,
 is equivalent to is equivalent to  , ,
then  for all values of for all values of  . .
That means that
 ---> --->
Although that gives you two choices for C,
it is a formula-driven, apparently less cumbersome, common strategy to solve all four problems.
Applying those formulas:
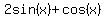 has has  ---> --->
The  angle in quadrant I that has angle in quadrant I that has 
measures approximately  (in radians). (in radians).
Using  and and  we would conclude that we would conclude that

We re-write the equations that 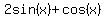 and solve: and solve:
(a)(i)  --> --> --> --> --> -->
 --> --> --> --> --> -->
(a)(ii) --> --> --> --> --> -->
 --> --> --> -->
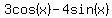 has has  ---> --->
The  angle in quadrant IV that has angle in quadrant IV that has 
measures approximately  (in radians). (in radians).
Using  and and  we would conclude that we would conclude that

We re-write the equations that 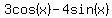 and solve: and solve:
(b)(i)  --> --> --> --> --> --> --> -->
--> --> -->
The two solutions are  and and
 , which can be written as , which can be written as  . .
(b)(ii)  <--> <--> --> --> --> -->
That means  --> --> --> -->
|
|
|