Question 870229: A river flows with a uniform velocity v. A person in a motorboat travels 1000m upstream, at which time a log is seen floating by. The person continues to travel upstream for 60.0min at the same speed and then returns downstream to the starting point, where the same log is seen again. Find the velocity of the river.
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! A river flows with a uniform velocity v. A person in a motorboat travels 1000m upstream, at which time a log is seen floating by. The person continues to travel upstream for 60.0min at the same speed and then returns downstream to the starting point, where the same log is seen again. Find the velocity of the river.
speed of current = v
distance traveled = 1000 m
time = 1 hour
boat speed = 1000m/hr
upstream speed = (1000-v)
distance traveled = 1000 m
t= 1000/(1000-v)
down stream speed = (1000+v)
distance = 2000 m
t= 2000/(1000+v)
total time to reach starting point = 1000/(1000-v)+ 2000/(1000+v)
Now the speed of log = v
distance = 1000 m
t= 1000/v
1000/v = 1000/(1000-v)+ 2000/(1000+v)
1000(1000^2-v^2)=1000v(1000+v)+2000v(1000-v)
10^9 -1000v^2=10^6v+1000v^2+2*10^6v-2000v^2
3*10^6v=10^9
v=10^9/3*10^6
100/3
333.33 mts/h
CHECK
Time for log to reach starting point
t=d/r
=1000/333=3.005 hour
Time for boat to go upstream
=1000/(1000-v)
=1000/667
=1.5 hours
time for boat to starting point
2000/(1000+v)
=2000/1333
=1.5 hours
boat time upstream + time downstream = 3 hours
Time for log to reach starting point =3.005 hours
Answer by ikleyn(52824)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A river flows with uniform velocity v. A person in a motorboat travels 1 km upstream,
at which time a log is seen floating by.
The person continues to travel upstream for one more hour at the same speed
and then returns downstream to the starting point, where the same log is seen again.
Find the velocity of the river.
~~~~~~~~~~~~~~~~~~~~~~~
The solution to this problem by @mananth in the archive is INCORRECT.
He incorrectly interpreted the problem and produced WRONG solution.
Ignore his post.
Below find my correct solution.
Let u be the speed of the boat in still water (in km/h).
and let v be the speed of the river ( == the speed of the current ).
(1) First, person travels 1 km upstream.
(2) At that time, he sees the log floating by. Let call this position "the meeting point".
(3) The person continue to travel upsteam for 1 more hour.
During this hour, the person travels (u-v) km upstream.
During this hour, the log travels v kilometers downstream with the current.
(4) Then the person turns back, travels downstream and reaches the starting point at the same time as the log comes to this point.
+----------------------------------------------+
| Let's consider kinematic, starting from |
| the "meeting point" to the ending moment. |
+----------------------------------------------+
During this time, the log travel 1 km with the current speed.
The motorboat travels 1 hour u-v kilometers upstream, and then travels ((u-v)+1)) kilometers DOWNSTREAM with the speed of (u+v) km/h.
So, the log's travel time from the meeting point to the end is  hours;
the motorboat's travel time from the meeting point to the end is hours;
the motorboat's travel time from the meeting point to the end is 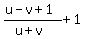 hours.
The two travel times are the same, giving this "time equation" hours.
The two travel times are the same, giving this "time equation"
 = = 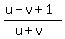 + 1 hours.
OK. The setup is done. Now our task is to solve the equation.
For it, multiply both sides by v*(u+v). You will get
u + v = v*(u-v+1) + v*(u+v)
u + v = vu - v^2 + v + vu + v^2
u = vu + vu
u = 2vu
Now divide both sides by u (which is not a zero, so we can divide safely) and get
1 = 2v
v = + 1 hours.
OK. The setup is done. Now our task is to solve the equation.
For it, multiply both sides by v*(u+v). You will get
u + v = v*(u-v+1) + v*(u+v)
u + v = vu - v^2 + v + vu + v^2
u = vu + vu
u = 2vu
Now divide both sides by u (which is not a zero, so we can divide safely) and get
1 = 2v
v =  .
The problem is just solved ( by a miraculous way (!) ).
ANSWER. The speed of the river (== the speed of the current) is .
The problem is just solved ( by a miraculous way (!) ).
ANSWER. The speed of the river (== the speed of the current) is  km/h. km/h.
Solved, and carefully explained.
/////////////
It is one of the classic, advanced and the most "delicious" Travel & Distance problems.
The key point in the solution is to get the setup equation, which I called "the time equation".
As soon as you get it, the rest is just a technique.
It is just a technique, but one miraculous moment still takes place (!)
This miraculous moment is the fact that the problem allows us to get a UNIQUE SOLUTION to equation in two unknowns ( ! )
Thanks to the mother-nature and to persons who invented/composed this miraculous problem many years ago ( ! )
|
|
|