Question 870024: I read through Question 869777, but did not understand the response given to it, is there perhaps another way of wording it? I appreciate the answer supplied, but can't seem to wrap my head around the concept
Can you help me to solve the following question:
The vertical displacement of the end of a robot arm (in mm) at time t (in seconds) is given by
y=1+4cos(2t)-4sin(4t)
a) find all times, t>0 (in exact form i.e. in terms of pi) where the vertical displacement is 1mm, i.e. y=1
b) what is the first time, t>0 that the vertical displacement is 1mm? give you answer exactly and to 2 decimal places?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  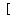 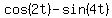  is a periodic function, waving above and below is a periodic function, waving above and below  , whose graph looks like this: , whose graph looks like this:
 Its period is Its period is  because at because at  and and 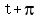 the function has the same the function has the same  value: value:
 . .
The function will take the value  an infinite number of times. an infinite number of times.
For an answer to part a) we can list the first few in order and then write ", ..." or we can write it as a formula.
Either way, it is not a simple answer.
The double angle trigonometric identity
 can be applied, with can be applied, with  to get to get
 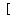 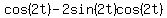 
Taking out  as a common factor, we get as a common factor, we get
  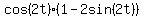 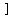

When will we have  ? ?
We have to solve
 <---> <--->
That will be true when one of those factors (either  or or  ) is zero. ) is zero.
 --> -->  or or  or anything you can get by adding or anything you can get by adding  to a previous answer. to a previous answer.
So  or or  or anything you can get by adding or anything you can get by adding  to a previous answer. to a previous answer.
 <---> <---> <---> <---> or or  or anything you can get by adding or anything you can get by adding  to a previous answer. to a previous answer.
That means  or or  or anything you can get by adding or anything you can get by adding  to a previous answer. to a previous answer.
a) The list of times when  is is
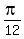    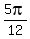       (and keep adding (and keep adding  to previous answers). to previous answers).
You could state that the answers are
 , ,  , ,  , and , and  , for any non-negative integer , for any non-negative integer  . .
I could not think of a simple and elegant way to express that as one formula.
b) The first time  happens when happens when 
|
|
|