|
Question 86995: PLEASE HELP ME I NEED HELP UNDERSTANDING HOW TO SOLVE THEM STEP BY STEP....
Problem #8
Which of the following investments is larger after 19 years?
(a) $7500 is deposited annually and earns 4.5% interest compounded annually.
(b) $600 is deposited monthly and earns 4.5% interest compounded monthly.
Problem #9
Find monthly payment.
In order to purchase a home, a family borrows $26000 at 10.8 % for 15 yr. What is their monthly payment? Round the answer to the nearest cent.
Found 2 solutions by stanbon, jim_thompson5910:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Problem #8
Which of the following investments is larger after 19 years?
(a) $7500 is deposited annually and earns 4.5% interest compounded annually.
(b) $600 is deposited monthly and earns 4.5% interest compounded monthly.
-------
Compare their growth using compound interest formula and the the Future Value formula:
Compound Interest: FV = (principal)(1+r/n)^(nt)
FV = 7500(1+0.045/1)^(1*19)
-------
Future Value: FV = (periodic payment)[(1+i)^n -1]/i
where periodic payment = $600; n=12*19 ; i=0.045/12
======================
Problem #9
Find monthly payment.
In order to purchase a home, a family borrows $26000 at 10.8 % for 15 yr. What is their monthly payment? Round the answer to the nearest cent.
--------
Use this annuity formla:
balance = (loan amt)(1+i)^n - [P/i][(1+i)^n - 1]
You want the balance to be zero;
loan amt=26000
i=0.108/12
n=12*15
Solve for P=monthly payment.
--------
I get $292.26
============
Cheers,
Stan H.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! #8
a)
Let p=7500, r=0.045, n=1, and t=19 and plug them into 
 Start with the given expression Start with the given expression
 Divide 0.045 by 1 to get 0.045 Divide 0.045 by 1 to get 0.045
 Multiply the exponents 1 and 19 to get 19 Multiply the exponents 1 and 19 to get 19
 Add 1 and 0.045 to get 1.045 Add 1 and 0.045 to get 1.045
 Raise 1.045 to the 19 th power to get 2.30786031084919 Raise 1.045 to the 19 th power to get 2.30786031084919
 Multiply 7500 and 2.30786031084919 to get 17308.9523313689 Multiply 7500 and 2.30786031084919 to get 17308.9523313689
So the return is $17,308.95
b)
Let p=600, r=0.045, n=12, and t=19 and plug them into 
 Start with the given expression Start with the given expression
 Divide 0.045 by 12 to get 0.00375 Divide 0.045 by 12 to get 0.00375
 Multiply the exponents 12 and 19 to get 228 Multiply the exponents 12 and 19 to get 228
 Add 1 and 0.00375 to get 1.00375 Add 1 and 0.00375 to get 1.00375
 Raise 1.00375 to the 228 th power to get 2.3476172358424 Raise 1.00375 to the 228 th power to get 2.3476172358424
 Multiply 600 and 2.3476172358424 to get 1408.57034150544 Multiply 600 and 2.3476172358424 to get 1408.57034150544
So the return is $1408.57
So the $7,500 investment is larger after 19 years
----------------------------------------------------------------------
#9
To calculate the monthly payment, use this formula:
 where P is the principal (i.e. the amount loaned out), R is the periodic interest rate (in decimal form) and n is the number of monthly payments where P is the principal (i.e. the amount loaned out), R is the periodic interest rate (in decimal form) and n is the number of monthly payments
First lets calculate R:
 To find the periodic interest rate, divide the APR (this is given as 10.8%) by the number of months in a year. Also divide the APR by 100 to convert the percentage to a decimal To find the periodic interest rate, divide the APR (this is given as 10.8%) by the number of months in a year. Also divide the APR by 100 to convert the percentage to a decimal
 Start with the given expression Start with the given expression
 Add Add 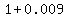 to get 1.009 to get 1.009
 Multiply Multiply 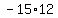 to get -180 to get -180
 Raise 1.009 to the -180 power Raise 1.009 to the -180 power
 Subtract Subtract 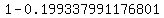 to get 0.800662008823199 to get 0.800662008823199
 Multiply Multiply 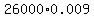 to get 234 to get 234
 Divide 234 by 0.800662008823199 to get 292.258153154949 Divide 234 by 0.800662008823199 to get 292.258153154949
So the monthly payment, rounded to the nearest cent, is roughly $292.26
|
|
|
| |