Question 86994:
Please help me solve this problem: the vertex
angle of an isosceles triangle is 57°24'
and each of its equal sides is 375.5 ft. long.
Find the altitude of the
triangle.
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! the vertex angle of an isosceles triangle is 57degrees 24 minutes and each of its equal sides is 375.5 ft. long. find the altitude of the triangle.
---------
Draw the picture.the vertex angle of an isosceles triangle is 57degrees 24 minutes and each of its equal sides is 375.5 ft. long. find the altitude of the triangle.
Each of the base angles is (1/2)(180 - 57 degrees 24') = (1/2)(122 degrees 36')
= 62 degrees 18'
Comment: 62 degrees 18' = 62.3 degrees
---------
Draw the altitude.
EQUATION:
sin(62.3) = altitude/375.5
altitude = 375.5*sin(62.3)
altitude = 332.47 ft.
============
Cheers,
Stan H.
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
Please help me solve this problem: the vertex
angle of an isosceles triangle is 57°24'
and each of its equal sides is 375.5 ft. long.
Find the altitude of the
triangle.
The solution by Stanbon contains an error in
calculation. He did it a different way, i.e.,
by calculating the base angles, but he calculated
the base angles as 62°18' and they should have
been 61°18'.
A triangle has three altitudes. I assume you
mean the altitude from the vertex angle to the
base.
Now draw in the altitude (call it "a") from the
vertex angle to the base.
The altitude divides the triangle into two
congruent right triangles, and divides the vertex
angle by 2. So each angle at the top is one-half of
57°24'. Since 57° is an odd number, and doesn't divide
evenly by 2, borrow one degree from the 57°,
making it an even number 56°, change the borrowed degree
to 60' and add it to the 24', giving 56°84':
57°48 ÷ 2 = 56°84' ÷ 2 = 28°42'
Now let's erase the right triangle on the right side
and just look at the one on the left:
The altitude "a" is the side adjacent to the 28°42' angle.
The side which is 375.5 feet is the hypotenuse. So you
need the basic trig function that involves adjacent and
hypotenuse, which is the cosine, so we have
cos(28°42') =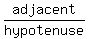 
cos(28°42') = 
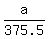Multiply both sides by 375.5
(375.5)cos(28°42') = a
The easiest way to handle 28°42' is to put the minutes
over 60 and add that to the number of degrees, that is,
enter
375.5 × cos(28 + 42/60)
on your calculator to get
a = 329.3683845. You should round
that to tenths since the given side
was rounded to tenths. So the
altitude from the vertex angle to the
base in the original isosceles triangle
is:
a = 329.4 ft.
Edwin
|
|
|
