|
Question 86891: 1. WhatÆs the smallest number that you can write with 1Æs and 0Æs which is divisible by 225?
2. The divisors of 216,000 add up to 792,480. What do their reciprocals add up to?
3. Find the product: 1À2À4À8À16À . . . À 2(to the 399th power)
4. All natural numbers from 1 to 101 are written in a row. How can the signs ô+ö and ô-ö be placed between them so that the value of the resulting expression is 0?
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. WhatÆs the smallest number that you can write with 1Æs and 0Æs which is divisible by 225?
The multiples of 225 end in 25, 50, 75, or 00. Only those ending in 00 could
contain only the digits 1's and 0's. Those are the multiples of 4Î225 or 900.
So we need a multiple of 900.
The multiples of 900 are just the multiples of 9 with two 0's annexed.
Theorem: A positive integer is divisible by 9 if and only if the sum of its digits is a multiple of 9.
So the smallest integer which contains only 1's and 0's and has sum of digits a multiple of 9 is 111111111 (9 1's). Then the smallest multiple of 900 that has only 1's and 0's is found by annexing two 0's to that. So the answer is 11111111100.
2. The divisors of 216,000 add up to 792,480. What do their reciprocals add up to?
Theorem: The sum of the reciprocals of positive integer n =
the sum of the divisors of n divided by n.
Let's do it with a smaller number like 12, so you can see why.
The divisors of 12 are 1,2,3,4,6,12. Their sum is 28.
Look at the sum of the reciprocals:

Obviously 12 is the LCD, so when we get the LCD of 12, we have
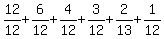
or
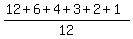
The numerator is just the sum of the divisors of 12, and
thus equals to the fraction 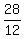 which reduces to 7/3 which reduces to 7/3
Let the set of divisors of 216,000 be S =
{1,2,3,4,5,6,8,9,10,12,15,16,18,20,...,216000}.
if x e S then 216000/x e S.
Look at this sum:

If we get the LCD of 216000, we have
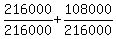 +...+ +...+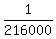
or the fraction
216000+108000+...+1
-------------------
`````216000
and the numerator is just the sum of the divisiors of 216000
which we are given to be 7982480.
So the answer is 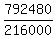 . Both numerator and . Both numerator and
denominator can be divided by 480 to reduce that fraction to
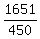
3. Find the product: 1À2À4À8À16À . . . À 2(to the 399th power)
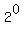 À À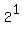 À À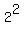 À À À À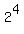 À...À À...À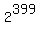
The sum of those exponents are the sum of the first 399 positive
integers.
The formula for the first n positive integers is 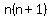
So the sum of the exponents is  = 79800, = 79800,
making the answer 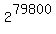
I'll come back to the last one. I haven't time just now.
Edwin
|
|
|
| |