please solve this problem: please solve the trigonometric equation
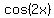 -
-  +
+  =
=  give all positive values of the angle between 0 to 360 degress
give any approximate value to the nearest minute only.
give all positive values of the angle between 0 to 360 degress
give any approximate value to the nearest minute only.
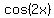 -
-  +
+  =
=  Multiply the equation through by LCD = 4
Multiply the equation through by LCD = 4
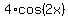 -
- 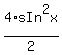 +
+ 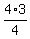 =
= 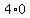 Simplifying:
Simplifying:
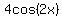 -
- 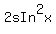 +
+  =
=  Use the identity cos 2q = 1 - 2sin²q
to substitute 1 - 2sin²x for cos(2x) in the first term:
Use the identity cos 2q = 1 - 2sin²q
to substitute 1 - 2sin²x for cos(2x) in the first term:
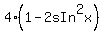 -
- 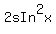 +
+  =
=  Remove the parentheses by distributing:
Remove the parentheses by distributing:
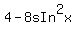 -
- 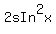 +
+  =
=  Combine like terms:
Combine like terms:
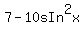 =
= 
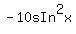 =
= 
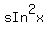 =
= 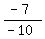
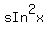 =
=  Take the square roots of both sides:
Take the square roots of both sides:
 = ±
= ±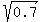
 = ±
= ±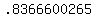 Find the inverse sine of .836600265 in the
first quadrant:
Find the inverse sine of .836600265 in the
first quadrant:
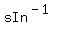
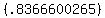 = 56.78908924°
To change the decimal part of that to minutes,
multiply the decimal part .78908924 by 60, getting
47.34535435' then round to the nearest minute, so
the value of x is the first quadrant is 56°47'.
But since the
= 56.78908924°
To change the decimal part of that to minutes,
multiply the decimal part .78908924 by 60, getting
47.34535435' then round to the nearest minute, so
the value of x is the first quadrant is 56°47'.
But since the  can be positive or
negative, we will get all the angles in all the
quadrants which have 56²47 as their reference
angles.
The second quadrant answer is found by
subtracting 56°47' from 180° or
180° - 56°47' = 179°60' - 56°47' = 123°13'
The third quadrant answer is found by
adding 56°47' to 180° or
180° + 56°47' = 236°47'
The fourth quadrant answer is found by
subtracting 56°47' from 360°
360° - 56°47' = 359°60' - 56°47' = 303°13'
So all the answers for x between 0° and 360° are
x = 56°47', 123°13', 236°47', and 303°13
Edwin
can be positive or
negative, we will get all the angles in all the
quadrants which have 56²47 as their reference
angles.
The second quadrant answer is found by
subtracting 56°47' from 180° or
180° - 56°47' = 179°60' - 56°47' = 123°13'
The third quadrant answer is found by
adding 56°47' to 180° or
180° + 56°47' = 236°47'
The fourth quadrant answer is found by
subtracting 56°47' from 360°
360° - 56°47' = 359°60' - 56°47' = 303°13'
So all the answers for x between 0° and 360° are
x = 56°47', 123°13', 236°47', and 303°13
Edwin