We draw the graph of y=4/x, by getting and plotting some points:
x|y
--|--
±1|±4
±2|±2
±3|±1.3
±4|±1
 Now the lines y=mx+4 will all have y intercept (0,4),
but will have different slopes. Here are some lines
that have the equation y=mx+4 where m has different
values
Now the lines y=mx+4 will all have y intercept (0,4),
but will have different slopes. Here are some lines
that have the equation y=mx+4 where m has different
values
 Some of those lines intersect the graph in 0 point, 1 points or 2 points.
The brownish-green line does not intersect it at all
The green and horizontal intersect the graph in 1 point
The purple and the light blue lines intersect the curve
in two points each.
If we solve the system of equations:
Some of those lines intersect the graph in 0 point, 1 points or 2 points.
The brownish-green line does not intersect it at all
The green and horizontal intersect the graph in 1 point
The purple and the light blue lines intersect the curve
in two points each.
If we solve the system of equations:
 by substitution, we get
by substitution, we get



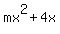


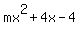

 What determines whether the line y=mx+4 intersects
the curve 0, 1, or 2 times, is whether this
quadratic equation has 0,1, or 2 real solutions.
And what determines whether a quadratic equation has
0, 1, or 2 real solutions is the DISCRIMINANT
What determines whether the line y=mx+4 intersects
the curve 0, 1, or 2 times, is whether this
quadratic equation has 0,1, or 2 real solutions.
And what determines whether a quadratic equation has
0, 1, or 2 real solutions is the DISCRIMINANT  .
.
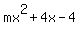

 a=m, b=4, c=-4 so the
discriminant =
a=m, b=4, c=-4 so the
discriminant =  =
= 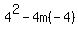 =
=  Case 1: If the discriminant is negative, there will be NO real solutions.
So we set the discriminant less than 0
Case 1: If the discriminant is negative, there will be NO real solutions.
So we set the discriminant less than 0
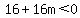
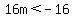
 So when m is less than -4, there will be NO solutions.
So we set the discriminant less than 0
So when m is less than -4, there will be NO solutions.
So we set the discriminant less than 0
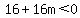
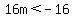
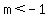 So when m is less than -1, there will be NO solutions.
and therefore the line will NOT intersect the curve at all.
Case 2: If the discriminant is EQUAL to zero, there will be ONE
real solution, and therefore the line will intersect the curve ONE time.
So we set the discriminant EQUAL to 0
So when m is less than -1, there will be NO solutions.
and therefore the line will NOT intersect the curve at all.
Case 2: If the discriminant is EQUAL to zero, there will be ONE
real solution, and therefore the line will intersect the curve ONE time.
So we set the discriminant EQUAL to 0


 So when m is equal to -1, there will be ONE real solutions.
and therefore the line will intersect the curve ONE time.
Case 3: If the discriminant is positive, there will be TWO real solutions.
So we set the discriminant GREATER than 0
So when m is equal to -1, there will be ONE real solutions.
and therefore the line will intersect the curve ONE time.
Case 3: If the discriminant is positive, there will be TWO real solutions.
So we set the discriminant GREATER than 0
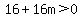
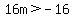
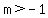 So when m is greater than -1, there will be TWO solutions,
and therefore the line will intersect the curve at TWICE.
Answer:
If the slope m < -1, the line y=mx+4 will intersect the curve 0 times.
If the slope m = -1, the line y=mx+4 will intersect the curve 1 time.
If the slope m > -1, the line y=mx+4 will intersect the curve 2 times.
Edwin
So when m is greater than -1, there will be TWO solutions,
and therefore the line will intersect the curve at TWICE.
Answer:
If the slope m < -1, the line y=mx+4 will intersect the curve 0 times.
If the slope m = -1, the line y=mx+4 will intersect the curve 1 time.
If the slope m > -1, the line y=mx+4 will intersect the curve 2 times.
Edwin