SOLUTION: 1. find the sum of the first 100 000 odd numbers. 2. find the greatest possible product of two natural numbers whose sum is 41.

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: 1. find the sum of the first 100 000 odd numbers. 2. find the greatest possible product of two natural numbers whose sum is 41.      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 868013: 1. find the sum of the first 100 000 odd numbers.
2. find the greatest possible product of two natural numbers whose sum is 41.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The first 100,000 odd numbers are the odd numbers from
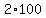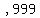2%2A1-1=2-1=1 to 2%2A100%22%2C000%22-1=200%22%2C000%22-1=199%22%2C999%22 :
1, 3, 5, .... 199,993, 199,995, 199,997, 199,999.
The sum of such an arithmetic sequence
(or arithmetic progression, if that's what it's called in your class)
is 100,000 =100000=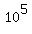10%5E5 (the number of terms in that sum)
times half the sum of the first and last terms,
%281%2B199999%29%2F2=200000%2F2=100000=10%5E5= 100,000.
So that sum is 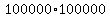100000%2A100000= 10,000,000,000,
or 10%5E5%2A10%5E5=10%5E10 .
Your teacher may want to see formulas.
I do not know what formulas you were taught,
and I believe in understanding concepts rather than memorizing and blindly applying formulas,
but I can throw a few formulas for you to use as needed.
The same concepts can be expressed in many different ways.
An arithmetic sequence has a first term a%5B1%5D,
and each term is the term before plus a common difference d ,
which can be written as
a%5Bn%5D=a%5Bn-1%5D%2Bd .
As a consequence
a%5B2%5D=a%5B1%5D%2Bd
a%5B3%5D=a%5B1%5D%2B2d
a%5Bn%5D=a%5B1%5D%2B%28n-1%29d ,
and of course, a%5Bn-1%5D=a%5B1%5D%2B%28n-2%29d
The sum of the first n terms is
S%5Bn%5D=a%5B1%5D%2Ba%5B2%5D%2B%22...%22%2Ba%5Bn-1%5D%2Ba%5Bn%5D=
That last expression contains a sum of n 2-term sums, and all the 2-term sums are equal:
,
.
So S%5Bn%5D=%281%2F2%29%28a%5B1%5D%2Ba%5Bn%5D%29%2An=n%2A%28%28a%5B1%5D%2Ba%5Bn%5D%29%2F2%29 .
That is the number of terms times half the sum of the first and last terms,
or (in other words) n times the average of the first and last terms.
An alternate formula is
S%5Bn%5D=%281%2F2%29%282a%5B1%5D%2B%28n-1%29d%29%2An .

If x is one of two natural numbers whose sum is 41 ,
then the other number is 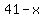41-x ,
and their product y is
y=%2841-x%29x=41x-x%5E2.
Traditionally, we prefer to rearrange the terms in the order y=-x%5E2%2B41x .
We notice that y is a quadratic function of x ,
and its graph would look like this,
graph%28300%2C300%2C-5%2C45%2C-500%2C500%2C-x%5E2%2B41x%29 , with a maximum.
To find the maximum we can "complete the square":
y=-x%5E2%2B41x<--->y=-%28x%5E2-41x%2B%2841%2F2%29%5E2%29%2B%2841%2F2%29%5E2<--->y=-%28x-41%2F2%29%5E2%2B%2841%2F2%29%5E2
Alternately, we can use the formula that says that the maximum for y=ax%5E2%2Bbx%2Bc occurs at x=-b%2F2a .
If we could use any rational value for x ,
the maximum would occur for x=41%2F2=20.5 ,
where we would have y=%2841%2F2%29%5E2=41%5E2%2F2%5E2=1681%2F4=420.25 .
However, since x must be a natural number,
the maximum value for the product will happen for the natural numbers x closest to 20.5 :
x=20 ---> 41-x=41-20=21
and x=21 ---> 41-x=41-21=20 .
IN either case, the product will be
20%2A21=highlight%28420%29