Write the complex number in rectangular form.
1.)  Just evaluate it:
Just evaluate it:
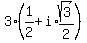
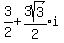 -----------------------------------------------------------------
-----------------------------------------------------------------
write the complex number in polar form. Express the argument theta in degrees, with 0 less than or equal to theta less than or equal to 360 degrees.
3√3 - 3i = x + iy,
where P(x,y) = P(3√3,-3),
Plot the point P(x,y) = P(3√3,-3),
draw a line from P to the origin,
and another line from P perpendicular to the x-axis.
Label the sides of the resulting right triangle x,y, and r,
Label the counter-clockwise angle q.
 Since the point P is P(x,y) = P(3√3,-3), x = 3√3 and y = -3.
We calculate r:
r² = x² + y²
r² = (3√3)² + (-3)².
r² = 9(3) + 9
r² = 27 + 9
r² = 36
r = √36
r = 6
Since the point P is P(x,y) = P(3√3,-3), x = 3√3 and y = -3.
We calculate r:
r² = x² + y²
r² = (3√3)² + (-3)².
r² = 9(3) + 9
r² = 27 + 9
r² = 36
r = √36
r = 6
 Therefore q = 330°,
since it is in Q4, with a reference angle of 30°.
Use
Therefore q = 330°,
since it is in Q4, with a reference angle of 30°.
Use  and
and  .
Solve them for x and y
.
Solve them for x and y
 and
and  x = 6*cos(330°) and y = 6*sin(330°)
So
3√3 - 3i = x + iy = 6*cos(330°) + i*6sin(330°) = 6(cos(330° + isin(330°)
--------------------------------------------------------------------------
convert the polar equation to rectangular form.
3.) r = 5
That is a circle at the origin (pole) with a radius of 5.
r² = x² + y²
5² = x² + y²
x² + y² = 25
Edwin
x = 6*cos(330°) and y = 6*sin(330°)
So
3√3 - 3i = x + iy = 6*cos(330°) + i*6sin(330°) = 6(cos(330° + isin(330°)
--------------------------------------------------------------------------
convert the polar equation to rectangular form.
3.) r = 5
That is a circle at the origin (pole) with a radius of 5.
r² = x² + y²
5² = x² + y²
x² + y² = 25
Edwin