Question 867018: David currently has a square garden He wants to redesign his garden and make into a rectangle with a length that is 3 feet shorter that twice its width. He decides that the perimeter should be 60 feet. Determine the dimensions, in feet, of his new garden. Thanks for your help.
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! w width, L length;
p perimeter.
L=2w-3 and 2w+2L=p
Try to symbolize further than that, k feet less than, and m times the width.
L=mw-k.
UNKNOWNS: L and w.
KNOWNS: p, m, k.
Solve for w and L.






-
Using the formula for w to solve for L is possible, but feeling it might maybe be more work than necessary, the choice will be to use the formula already for L and the p formula, and just do according to the method used in finding w.
 , ,

 . .









SUBSTITUTE THE VALUES FOR k, m, and p;
m=2, k=3, p=60.
COMPUTE w AND L.
(*) If you have more than one problem which fits this same form, you can use the very same symbolic form solutions for w and L.
(*) Using the given values from the description at the beginning might be easier and much faster than turning everything into pure symbolism in variables, but this would be solved only for one single example and none others.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! David currently has a square garden He wants to redesign his garden and make into a rectangle with a length that is 3 feet shorter that twice its width. He decides that the perimeter should be 60 feet. Determine the dimensions, in feet, of his new garden. Thanks for your help.
Let width of new garden be W
Then length of new garden = 2W - 3
Thus, 2(W) + 2(2W - 3) = 60
2W + 4W - 6 = 60
6W = 66
W, or width = 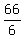 , or 11 , or 11
Length of new garden: 2(11) - 3, or 22 - 3, or  feet feet
You can do the check!!
Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.
Further help is available, online or in-person, for a fee, obviously.
|
|
|