Question 866140: A family has 4 children. Using a tree diagram that shows how many ways the children could have been born, from first to last born, determine how many ways the family could have had 2 boys and 2 girls. Then find the probability of having 2 boys and 2 girls.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is a tree diagram depicting all the possible ways to have 4 kids

The first column (of just 2 choices) represents child #1.
If we stop at the second column, and ignore everything past it, then we see that there are 2^2 = 4 ways to have 2 kids (and those ways are shown in the tree diagram)
Likewise, if we stop at column #3, then we see all the possible ways to have 3 kids (2^3 = 8 different ways)
The last column is that last and 4th child. There are 2^4 = 16 ways to have 4 kids. Each possible path you trace (from the starting node to either a B or G in the fourth column) generates a sequence of 4 letters (either B or G) that represents a combination of boys and/or girls. For example, trace along the very top branches and you'll only pick up B, B, B, B or BBBB which represents all 4 kids being boys.
-----------------------------------------------------------------
Let's highlight all of the paths that have exactly 2 boys and exactly 2 girls.
Here is one path

This is the sequence BBGG which means the first two kids are boys, the second 2 are girls (boy, boy, girl, girl)
------------------------------------
Here is another

That is the sequence BGBG (boy, girl, boy, girl)
------------------------------------
Here is another

This sequence is BGGB (boy, girl, girl, boy)
------------------------------------
and here is another path of exactly 2 girls, 2 boys

This sequence is GBBG (girl, boy, boy, girl)
------------------------------------
and here is another path of exactly 2 girls, 2 boys

This sequence is GBGB (girl, boy, girl, boy)
------------------------------------
and finally, here is the last path that represents exactly 2 girls, 2 boys

This sequence is GGBB (girl, girl, boy, boy)
----------------------------------------------------------
----------------------------------------------------------
There are 6 sequences highlighted above and they are
BBGG
BGBG
BGGB
GBBG
GBGB
GGBB
So there are 6 ways to have 2 boys and 2 girls (they are shown above).
-------------------------
To calculate the probability of having 2 boys and 2 girls, you divide that last number we found (6) by 16. This is because there are 16 ways to have 4 kids (2^4 = 16)
So, 
The answer as a fraction is 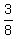
Now use a calculator to get 
The answer as a decimal is 0.375
And multiply that decimal result by 100 to convert it over to a percentage 0.375*100 = 37.5%
The answer as a percentage is 37.5%
|
|
|