Question 866123: a rectangle has a length that is 5 less than twice the width.if the rectangle has an area of 63, find the length and width.
I am having trouble figuring out how to set up this problem I would be very grateful if someone could help me.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = width of the rectangle (in whatever units of length they use) = width of the rectangle (in whatever units of length they use)
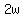 = twice the width = twice the width
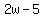 = length of the rectangle (it is 5 less than twice the width) = length of the rectangle (it is 5 less than twice the width)
The area of the rectangle is length times width, so it is

That is the equation to solve, but we re-arrange it.



Now it looks like a standard  quadratic equation and we can solve it using the quadratic formula: quadratic equation and we can solve it using the quadratic formula:
 , ,
except that instead of  we have we have  , and we have , and we have
 , ,  , and , and  , so , so

The two solutions for  are are
 and and
(5 - 23)/4=-18/4=-9/2}}} ,
but since the width of the rectangle must be a positive number,
we must discard  , and the solution is , and the solution is
 , along with , along with

The same  quadratic equation can be solved by other means. quadratic equation can be solved by other means.
Ypu could "complete the square" (not so easy),
or you could solve it by factoring 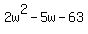 (if you are good at factoring). (if you are good at factoring).
Factoring:

so  can be written as can be written as  , ,
which is true if  , ,
and those two options lead us to the solutions
 found above. found above.
Completing the square:
 <--> <-->
dividing both sides of the equal sign by 2,





So 
which means that

|
|
|