Question 865985: Question: Find all angles theta (I don't have a symbol for that) in radians on the interval [0,4pi] such that cos(theta) = 1/2.
I think I have to set a up graph from 0 to 4pi and draw a wavy line and determine at what points x crosses y=1/2. It that correct? How do I do that?
Found 2 solutions by josmiceli, rothauserc:
Answer by josmiceli(19441)   (Show Source): (Show Source):
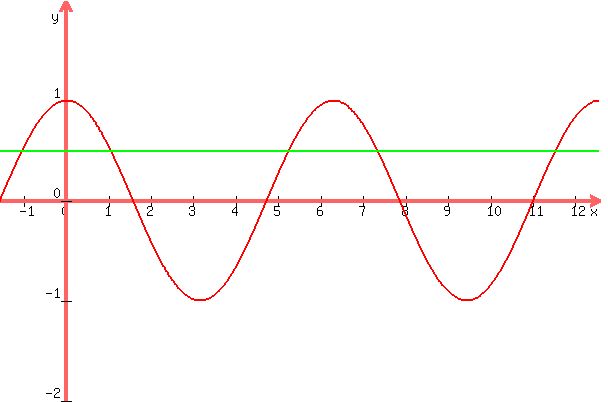
You can put this solution on YOUR website! Plot 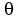 on the horizontal axis and on the horizontal axis and
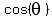 on the vertical axis. on the vertical axis.
----------------------------------
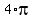 is two cycles of the cos wave. is two cycles of the cos wave.
The cos starts out at +1, then goes to zero,
then to -1, then back to zero ( 1 complete cycle )
-------------------------------------------
The only places where the cos is positive is
the 1st quadrant and the 4th quadrant.
If  , then , then
 and, also and, also

--------------------------------
To get all the angles from  to to 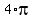 , ,
You just have to add  to these to these
------------------------------------
 and and

--------------------------------
So, the answers are:
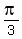 , , 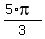 , , 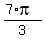 , and , and 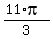
---------------------------------
Here's the plot:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! 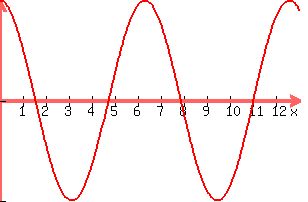
note that pi = 180 degrees, therefore the interval in degrees is [0, 720]
the cosine of 60 degrees is 1/2
we convert degrees to radians = degrees * pi/180
60 degrees = pi/3 radians
from the graph, we see the following
the angles theta in radians are pi/3, 5*pi/3, 7*pi/3, 11*pi/3
|
|
|