Find the polar coordinates of the point whose rectangular coordinates are
(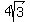 , -4)
, -4)
We will indicate the rectangular coordinates of point P in
black as 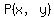 and the polar coordinates of point P
in red as
and the polar coordinates of point P
in red as 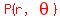 Plot P using its rectangular coordinates
Plot P using its rectangular coordinates 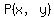 = (
= (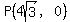 :
:
 The x-coordinate of point P is
The x-coordinate of point P is  and the y-coordinate
of point P is -4.
Draw a right triangle with this point P and the origin as
vertices and the right angle on the x-axis. The legs of this right
triangle x and y are the RECTANGULAR coordinates of point P. The
hypotenuse r of this right triangle is the first POLAR coordinate
of P. The angle
and the y-coordinate
of point P is -4.
Draw a right triangle with this point P and the origin as
vertices and the right angle on the x-axis. The legs of this right
triangle x and y are the RECTANGULAR coordinates of point P. The
hypotenuse r of this right triangle is the first POLAR coordinate
of P. The angle  indicated by the counter-clockwise red
arc is the second POLAR coordinate of the point
indicated by the counter-clockwise red
arc is the second POLAR coordinate of the point 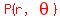
 We only need to calculate
We only need to calculate  and
and 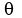






 Therefore
Therefore 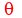 in the 4th quadrant is
in the 4th quadrant is 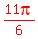 , and
, and
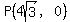 =
= 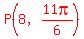

Find the rectangular coordinates of the point whose polar coordinates are
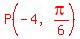 .
.
Let's draw the point 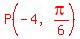 using its polar coordinates.
First we draw the angle
using its polar coordinates.
First we draw the angle 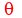 with a dotted line through
the origin:
with a dotted line through
the origin:
 Next we locate the value of r on the x-axis, then we swing an
arc from that point on the x-axis around to the dotted line,
like the green arc below swinging from -4 on the x-axis to
the dotted line, and mar that point
Next we locate the value of r on the x-axis, then we swing an
arc from that point on the x-axis around to the dotted line,
like the green arc below swinging from -4 on the x-axis to
the dotted line, and mar that point 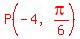 .
.
 Then we erase the green arc and draw a right triangle with
this point P and the origin as vertices and the right angle
on the x-axis, and indicate the RECTANGULAR coordinates x,
y, of the point P. Since we swung the point from the point
x=-4, the hypotenuse
Then we erase the green arc and draw a right triangle with
this point P and the origin as vertices and the right angle
on the x-axis, and indicate the RECTANGULAR coordinates x,
y, of the point P. Since we swung the point from the point
x=-4, the hypotenuse  .
.
 Now we calculate x and y.
Now we calculate x and y.









 So
So 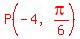 =
= 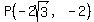

Find a rectangular form of the equation 
Always substitute trig functions first,
 ,
,  ,
,  and always wait until last to replace
and always wait until last to replace  by
by 





 You can then put it in standard form of a circle,
You can then put it in standard form of a circle,
 getting:
getting:
 whose graph is a circle with center (h,k) = (
whose graph is a circle with center (h,k) = ( ,0)
and radius
,0)
and radius  :
:
 Edwin
Edwin