SOLUTION: I previously asked this question and got this solution (after question). But I would appreciate further clarification. The line with the equation y=mx is tangent to the circle wit

Algebra ->  Coordinate-system -> SOLUTION: I previously asked this question and got this solution (after question). But I would appreciate further clarification. The line with the equation y=mx is tangent to the circle wit      Log On


   

Question 864960: I previously asked this question and got this solution (after question). But I would appreciate further clarification.
The line with the equation y=mx is tangent to the circle with centre (-8,0) and radius 4 at the point P(x,y). 
a)find x coordinate of P in terms of m 
b)Show that m = +- sqrt (3)/ 3 and hence find the coordinates of P
(x+8)^2+y^2=16
(x+8)^2+y^2=16, y=mx
m = 1/sqrt(3),   x = -6,   y = m x
m =-1/sqrt(3),   x = -6,   y = m x
+-1/sqrt(3)=+-sqrt(3)x/3
y=+-sqrt(3)x/3
x=-6,   y =2sqrt(3)
P=(-6,2sqrt(3))
Can you please provide further clarification- 
Step 3 and 4-
m = 1/sqrt(3), x = -6, y = m x 
m =-1/sqrt(3), x = -6, y = m x 
How was the x coordinate found. 
Step 5 
+-1/sqrt(3)=+-sqrt(3)x/3 
what is happening here for one to become the other.
I need this explained very simply So i i can understand it. Especially my queries about the steps. Thank you very much.

Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
I just did this for you last night. Did you not understand my explanation?


Same as question 864931
http://www.algebra.com/algebra/homework/Linear-equations/Linear-equations.faq.question.864931.html

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I see several ways to get the answer. I cannot tell if one of the ways I would use was used in the first answer you got. Maybe the reasoning was through a different way. I can explain one or more ways. However, I am a long-winded explainer, so you may get more explanation that you bargained for.

USING GEOMETRY AND ANALYTIC GEOMETRY:
The tangent to a circle is perpendicular to the radius at the point of tangency, so I would draw the sketch like this:
The tangents, radii, and the x-axis form right triangles OPC and OQC.
The two triangles are congruent, with P(x,y) and Q(x,-y), so I only need to solve OPC.
I know that the length of leg CP is 4, and the hypotenuse OC is 8 .
sin%28theta%29=4%2F8=1%2F2
That tells me that the angle theta measures 30%5Eo
and OPC is a 30-60-90 triangle.
From the tangent of that 30%5Eo angle you can also get the slopes of the tangents.
.
We multiply times 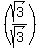%28sqrt%283%29%2Fsqrt%283%29%29 because we do not like to see square roots in denominators,
so m = +- sqrt%283%29%2F3 .
Of course, OP is the line with the negative slope, and OQ is the line with the positive slope.
For OP, y=%28-sqrt%283%29%2Fsqrt%283%29%29%29x and
for OQ, y=%28sqrt%283%29%2Fsqrt%283%29%29%29x .
The altitude of that right triangle splits it into two similar right triangles, CPM, and OPM.
As the ratio of short leg to hypotenuse for OPC is 4%2F8=1%2F2, the ratio is also the same for CPM, and OPM, so
CM=4%2A%281%2F2%29=2 and the x-coordinate of points M and P (and Q) is -8%2B2=highlight%28-6%29
For OP, y=%28-sqrt%283%29%2Fsqrt%283%29%29%29x
and for P, y=mx=m%2A%28-6%29=%28sqrt%283%29%2Fsqrt%283%29%29%2A%28-6%29=2sqrt%283%29 .
On the other hand, for Q, y=-2sqrt%283%29 .

WITHOUT MENTIONING GEOMETRY (too much):
OK, we need to know the equation of the circle, and I could call that analytical geometry, but you learn that in algebra 2 too.
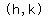The equation of a circle with radius r and center at %22%28+h+%2C+k+%29%22 is
%28x-h%29%5E2%2B%28y-k%29%5E2=r%5E2 .
For the circle in your problem, that would be
%28x-%28-8%29%29%5E2%2B%28y-0%29%5E2=4%5E2 ---> %28x%2B8%29%5E2%2By%5E2=16 ---> x%5E2%2B16x%2B64%2By%5E2=16
If y=mx is tangent to the circle, there is only one point in common to circle and line,
so system%28x%5E2%2B16x%2B64%2By%5E2=16%2Cy=mx%29 has one and only one solution.
system%28x%5E2%2B16x%2B64%2By%5E2=16%2Cy=mx%29-->x%5E2%2B16x%2B64%2B%28mx%29%5E2=16-->x%5E2%2B16x%2B64%2Bm%5E2x%5E2=16-->%28m%2B1%29x%5E2%2B16x%2B64-16=0-->%28m%2B1%29x%5E2%2B16x%2B48=0
For what value of m would that quadratic equation have one and only one solution?
A quadratic ax%5E2%2Bbx%2Bc=0 has one and only one real solution when b%5E2-4ac=0 ,
and then x=-b%2F2a
In the case of %28m%2B1%29x%5E2%2B16x%2B48=0 ,
b=16 , a=m%5E2%2B1 , and c=48 .
It will have one and only one real solution when
16%5E2-4%2A%28m%5E2%2B1%29%2A48=0-->16%5E2=4%2A48%2A%28m%5E2%2B1%29-->16%2A16=4%2A3%2A16%2A%28m%5E2%2B1%29-->16%2Across%2816%29=4%2A3%2Across%2816%29%2A%28m%5E2%2B1%29-->16=12%28m%5E2%2B1%29
So m%5E2%2B1=16%2F12-->m%5E2%2B1=4%2F3-->m%5E2=4%2F3-1-->m%5E2=1%2F3
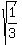m = +-sqrt%281%2F3%29= +- 1%2Fsqrt%283%29= +- sqrt%283%29%2F3 .
In either case, we can use x=-b%2F2a to find the same x value:
m%5E2%2B1=4%2F3 --> highlight%28x=%28-16%29%2F%28m%5E2%2B1%29%29
That is the "x coordinate of P in terms of m" as your problem asked for.
Maybe this is the way your teacher/book expected you to solve the problem.
We can calculate further (apparently not required by your problem):
x=-16%2F%28%284%2F3%29%29=-16%2A%283%2F4%29=-6