Question 864194: Find all rational, irrational and complex solutions for:

I know by Descartes' rule of zeros (and solving) that there should be 2 positive values for x : 1/2 and 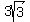
There should also be two negative values as well.. how do I find them?
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! we are given 2x^4 -x^3 -6x + 3 = 0
I usually check or x = 1 or -1 first
2 - 1 -6 +3 = -2 so x = 1 is not a 0
2 + 1 +6 +3 = 12 so x = -1 is not a 0
now for the rational roots test (factors of the constant term / factors of leading coefficient, then possible 0's are 1, 1/2, 3, 3/2
+ or - 3,1 / 2, 1 = 1, 1/2, 3, 3/2
now is a good time to consult a graph of the equation, where is crosses the x axis will be 0's
the graph crosses the x axis at 1/2 but does not cross x axis < 0
use x = 1/2 for synthetic division
1/2 | 2 -1 0 -6 3
| 1 0 0 -3
| 2 0 0 -6 0
this leaves us with
2x^3 -6 which is the decompression polynomial
x = 3^(1/3)
apply synthetic division to our decompression polynomial
3^(1/3) | 2 0 0 -6
| 2*3^(1/3) 2*3^(2/3) 6
| 2 2*3^(1/3) 2*3^(2/3) 0
this leaves us with
2x^2 + 2*3^(1/3)x + 2*3^(2/3) = 0
x^2 + 3^(1/3)x + 3^(2/3) = 0
use quadratic formula to solve for x
x = [ -b ± √ ( (b)^2 - 4(a)(c) ) ] / 2(a)
x = [ -3^(1/3) ± √ ( (3^(1/3))^2 - 4(1)(3^(2/3)) ) ] / 2(1)
x = [ -3^(1/3) ± √ ( 3^(2/3) - 4(3^(2/3)) ] / 2
x = [ -3^(1/3) ± √ ( - 3 (3^(2/3) ) ] / 2
x = [ -3^(1/3) ± 3^(1/3) √ ( - 3) ] / 2
x = (1/2) 3^(1/3) [ -1 ± √3 i ]
therefore our solutions are
x = 1/2, 3^(1/3), (1/2) 3^(1/3) [ -1 ± √3 i ]
|
|
|