SOLUTION: A cylindrical container is to have a volume of 100 pi square inches. Suppose that the material for the curved side costs twice as much

Algebra ->  Surface-area -> SOLUTION: A cylindrical container is to have a volume of 100 pi square inches. Suppose that the material for the curved side costs twice as much       Log On


   

Question 864008: A cylindrical container is to have a volume of 100 pi square inches. Suppose that the material for the curved side costs twice as much as the material for the top, while the material for the bottom costs three times as much as the material for the top. Find the dimensions of the cylinder that minimize cost of construction.
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
Surface Area: 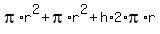pi%2Ar%5E2%2Bpi%2Ar%5E2%2Bh%2A2%2Api%2Ar, using h for length top to bottom.

Material Prices: Each refers to the material for the top.
Top, x money units per square inch
Curved Side, 2x
Bottom, 3x

Account for Material Cost: 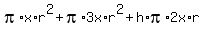pi%2Ax%2Ar%5E2%2Bpi%2A3x%2Ar%5E2%2Bh%2Api%2A2x%2Ar
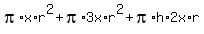
pi%2Ax%2Ar%5E2%2Bpi%2A3x%2Ar%5E2%2Bpi%2Ah%2A2x%2Ar

A function for material cost for the cylinder is wanted, and we have two variables, h and r. We are assuming x is known, so it is a constant. We can use the given volume 100*pi to find a formula for h:

h%2Api%2Ar%5E2=100%2Api
h=100%2Fr%5E2
Substitute into the Material Cost expression to make the function.
C=pi%2Ax%2Ar%5E2%2Bpi%2A3x%2Ar%5E2%2Bpi%28100%2Fr%5E2%29%2A2x%2Ar
We do not need to specifically know any particular value for x; it is "the money unit" and for all practical purposes, since the ratios were already given, x=1...
C=pi%2Ar%5E2%2Bpi%2A3r%5E2%2Bpi%2A2%28100%2Fr%5E2%29r
C=pi%28r%5E2%2B3r%5E2%2B2%2A100%2Fr%29
highlight_green%28C=pi%284r%5E2%2B200%2Fr%29%29
We should be able to look for r-axis intercepts, treating r as the horizontal number line. ...Maybe not...

highlight%28C=pi%284r%5E2%2Ar%2B200%29%2Fr%29
highlight%28C=pi%284r%5E3%2B200%29%2Fr%29
-
Either form of this C function would do; this seems to be a Calculus derivative problem. Find first derivative, and look for a minimum value where the derivative is zero.
I resorted to Google to look at the graph instead of actually finding and using the derivative. The minimum looks like it is around r=3 for the minimum cost.