SOLUTION: Find the area of an isoceles trapeziod that has a perimeter of 90 meters. The longer base is 5 meters less than twice the length of the shorter base. The length of each leg is 3 me

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: Find the area of an isoceles trapeziod that has a perimeter of 90 meters. The longer base is 5 meters less than twice the length of the shorter base. The length of each leg is 3 me      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 863534: Find the area of an isoceles trapeziod that has a perimeter of 90 meters. The longer base is 5 meters less than twice the length of the shorter base. The length of each leg is 3 meters less than the length of the shorter base.
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
b, bottom base, the longer base
t, top base
y, each side
-
b=-5%2B2t
and
y=-3%2Bt
-
SUM of the lengths of the sides is 90 meters, according to "perimeter of 90 meters". Notice how b and y are described in terms of t.

90=%28-5%2B2t%29%2Bt%2B2%28-3%2Bt%29
-6%2B2t%2Bt%2B2t-5=90
5t-11=90
5t=101
highlight%28t=101%2F5%29.

The base angle at bottom is needed, so that the height can be found. This isosceles trapezoid is composed of two right triangles, one on each side, and a rectangle in the middle. You can draw this figure.

Call the base angle, measure a.
Let h = height of the triangle and also of the trapezoid.
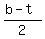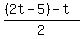
The bottom leg OF EACH RIGHT TRIANGLE is %28b-t%29%2F2; and since you have a formula for b and have now found t, each bottom leg of the right triangle is %28%282t-5%29-t%29%2F2
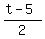
%28t-5%29%2F2
%28101%2F5-5%29%2F2
%28101-25%29%2F%285%2A2%29
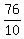
76%2F10
highlight_green%2838%2F5%29, leg length of a right triangle.
-
The hypotenuse of each right triangle is y.
cos%28a%29=%2838%2F5%29%2Fy, and a formula for y is already described in terms of t.
%2838%2F5%29%2F%28t-3%29=cos%28a%29
%2838%2F5%29%2F%28101%2F5-3%29=cos%28a%29
%2838%2F5%29%2F%28101%2F5-15%2F5%29=cos%28a%29
%2838%2F5%29%2F%2886%2F5%29=cos%28a%29
cos%28a%29=38%2F86
highlight%28a=63.8%29 degrees
-
highlight%28h=y%2Asin%2863.8%29%29
h=%28t-3%29sin%2863.8%29
h=%28101%2F5-3%29sin%2863.8%29
highlight%28h=%2886%2F5%29sin%2863.8%29%29-----The HEIGHT of the trapezoid.

AREA:
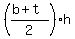
%28%28b%2Bt%29%2F2%29h
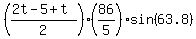
%28%282t-5%2Bt%29%2F2%29%2886%2F5%29sin%2863.8%29
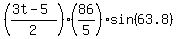
%28%283t-5%29%2F2%29%2886%2F5%29sin%2863.8%29
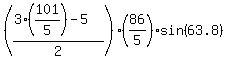
%28%283%28101%2F5%29-5%29%2F2%29%2886%2F5%29sin%2863.8%29
.... you can finish this computation.