Question 863090: suppose p(x)=-x^2+30x-50 is the profit P(x),in thousands of dollars, for a firm when it sells x thousand units
a) What is the firm profit when it sells 1000 units
b) What is the firms profit when it sells 10,000 units
c) how many units must the firm sell to break even
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
profit P(x),in thousands of dollars, for a firm when it sells x thousand units
p(x)= -x^2+30x-50
a) What is the firm profit when it sells 1000 units: p(1) = 29-50 = -$21,000
b) What is the firms profit when it sells 10,000 units: p(10) = $150,000
c) how many units must the firm sell to break even: 1772 units
-x^2+30x-50 = -(x-15)^2 + 175
x = 1.77124, 28.22875
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=700 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 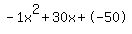 can be factored: can be factored:

Again, the answer is: 1.77124344467705, 28.228756555323.
Here's your graph:
 |
|
|
|