SOLUTION: An arrow is shot vertically upward from a platform 10 ft high at a rate of 185 ft per sec. When will the arrow hit the ground? Use the formula: h=16t^2+vt+h. (round off answer to t

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: An arrow is shot vertically upward from a platform 10 ft high at a rate of 185 ft per sec. When will the arrow hit the ground? Use the formula: h=16t^2+vt+h. (round off answer to t      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 862633: An arrow is shot vertically upward from a platform 10 ft high at a rate of 185 ft per sec. When will the arrow hit the ground? Use the formula: h=16t^2+vt+h. (round off answer to the nearest tenth. Find seconds.
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!


Hi

h= -16t^2+185t+10, h = 0 when it hits the ground

 16t^2+185t+10 = 0

t = 11.6sec (to nearest tenth)

  


 
Solved by pluggable solver: SOLVE quadratic equation with variable


Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case -16x%5E2%2B185x%2B10+=+0) has the following solutons:

  

  x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

  

  For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

  

  First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28185%29%5E2-4%2A-16%2A10=34865.

  

  Discriminant d=34865 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-185%2B-sqrt%28+34865+%29%29%2F2%5Ca.

  

    x%5B1%5D+=+%28-%28185%29%2Bsqrt%28+34865+%29%29%2F2%5C-16+=+-0.0538036897701293

    x%5B2%5D+=+%28-%28185%29-sqrt%28+34865+%29%29%2F2%5C-16+=+11.6163036897701

    

    Quadratic expression 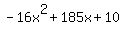-16x%5E2%2B185x%2B10 can be factored:

  -16x%5E2%2B185x%2B10+=+-16%28x--0.0538036897701293%29%2A%28x-11.6163036897701%29

  Again, the answer is: -0.0538036897701293, 11.6163036897701.
Here's your graph:

graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+-16%2Ax%5E2%2B185%2Ax%2B10+%29