<
I need help with these problems, most of them do need to be graphed. I want to
thank the person who helps out. Thank you and I really am grateful.
Solve the system by graphing.
3x+y=6
3x-y=0
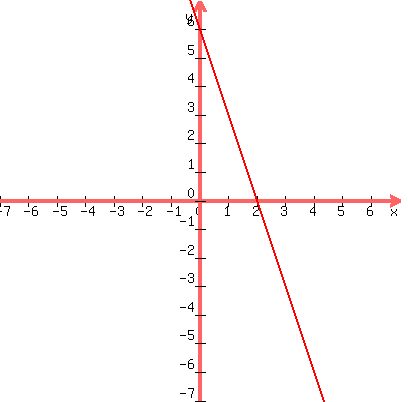
The intercepts of the first line are (0,6) and (2,0). So plot
those two points and draw a line through them:
 The only intercept of the second line is (0,0) so we must find
another point. Choose, say x = 1 then
3x - y = 0
3(1) - y = 0
3 - y = 0
-y = -3
y = 3
So plot (0,0) and (1,3) and draw a green line through them
The only intercept of the second line is (0,0) so we must find
another point. Choose, say x = 1 then
3x - y = 0
3(1) - y = 0
3 - y = 0
-y = -3
y = 3
So plot (0,0) and (1,3) and draw a green line through them
 Through the point where those two line cross, draw a
dotted horizontal line
Through the point where those two line cross, draw a
dotted horizontal line
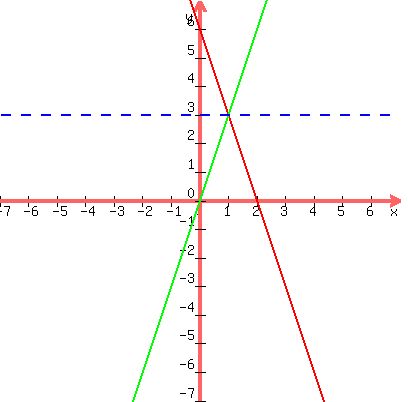 Through the point where those two line cross, draw a
horizontal line
Through the point where those two line cross, draw a
horizontal line
 Also draw a vertical line through the point where they cross:
Also draw a vertical line through the point where they cross:
 Notice that the vertical line cuts the x-axis at 1, and
the horizontal line cuts the y-axis at 3. So the solution of the system
is (x,y) = (1,3)
Check by substituting into both equations:
Substituting in the first equation:
3x + y = 6
3(1) + 3(3) = 6
3 + 3 = 6
6 = 6
That's true.
Substituting in the first equation:
3x - y = 0
3(1) - (3) = 0
3 - 3 = 0
0 = 0
That's also true. So we know (x,y) = (1,3)
is the correct solution to the system
3x + y = 6
3x - y = 0
--------------------------
Solve the following system of linear inequalities by graphing.
3x - y < 2
x + y < 2
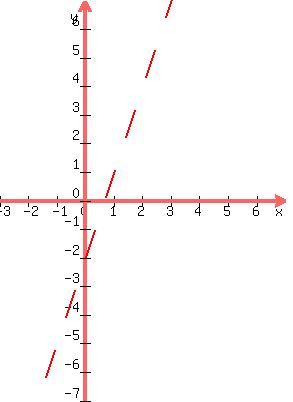
We draw the boundary line for the first one. We draw it
dotted because it's "<" and not "<". The equation
of the boundary line is 3x - y = 2.
Two points on it are (0,-2) and (1,1). So we plot those
and draw a dotted line through them:
Notice that the vertical line cuts the x-axis at 1, and
the horizontal line cuts the y-axis at 3. So the solution of the system
is (x,y) = (1,3)
Check by substituting into both equations:
Substituting in the first equation:
3x + y = 6
3(1) + 3(3) = 6
3 + 3 = 6
6 = 6
That's true.
Substituting in the first equation:
3x - y = 0
3(1) - (3) = 0
3 - 3 = 0
0 = 0
That's also true. So we know (x,y) = (1,3)
is the correct solution to the system
3x + y = 6
3x - y = 0
--------------------------
Solve the following system of linear inequalities by graphing.
3x - y < 2
x + y < 2
We draw the boundary line for the first one. We draw it
dotted because it's "<" and not "<". The equation
of the boundary line is 3x - y = 2.
Two points on it are (0,-2) and (1,1). So we plot those
and draw a dotted line through them:
 No we choose a test point which can be any point not on the line.
We pick the point (0,0) since it is the easiest point not on the line.
We substitute it in the INEQUALITY
3x - y < 2
3(0) - (0) < 2
0 < 2
This is true, so we will shade the side of the line which the
origin (0,0) is on. That means we will shade the LEFT (upper) side of
the line because the test point, which is the origin (0,0), is
a point on the LEFT (upper) side of the line which contains the solutions
to the inequality.
Now we draw the boundary line for the second one. We also draw it
dotted because it's "<" and not "<". The equation
of the boundary line is x + y = 2.
Two points on it are (0,2) and (2,0). So we plot those
and draw a dotted line through them:
No we choose a test point which can be any point not on the line.
We pick the point (0,0) since it is the easiest point not on the line.
We substitute it in the INEQUALITY
3x - y < 2
3(0) - (0) < 2
0 < 2
This is true, so we will shade the side of the line which the
origin (0,0) is on. That means we will shade the LEFT (upper) side of
the line because the test point, which is the origin (0,0), is
a point on the LEFT (upper) side of the line which contains the solutions
to the inequality.
Now we draw the boundary line for the second one. We also draw it
dotted because it's "<" and not "<". The equation
of the boundary line is x + y = 2.
Two points on it are (0,2) and (2,0). So we plot those
and draw a dotted line through them:
 No we choose a test point which can be any point not on the line.
We pick the point (0,0) again since it is the easiest point not on
the line.
We substitute it in the INEQUALITY
x + y < 2
0 + 0 < 2
0 < 2
This is true, so we will shade the side of the line which the
origin (0,0) is on. That means we will shade the lower or LEFT side of
the line because the test point, which is the origin (0,0), is
a point on the lower LEFT side of the line which contains the solutions
to the inequality.
Now to shade the solution set. We shade the region which is LEFT of
both lines.
No we choose a test point which can be any point not on the line.
We pick the point (0,0) again since it is the easiest point not on
the line.
We substitute it in the INEQUALITY
x + y < 2
0 + 0 < 2
0 < 2
This is true, so we will shade the side of the line which the
origin (0,0) is on. That means we will shade the lower or LEFT side of
the line because the test point, which is the origin (0,0), is
a point on the lower LEFT side of the line which contains the solutions
to the inequality.
Now to shade the solution set. We shade the region which is LEFT of
both lines.
 Solve the following system of linear inequalities bt graphing
x - y < 3
x + 2y > 6
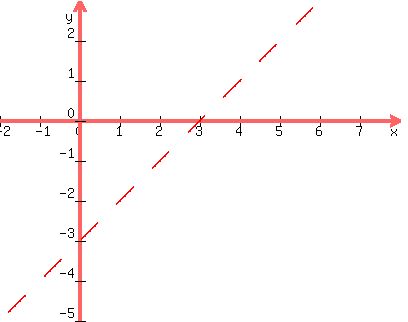
Draw the first boundary line dotted:
x - y = 3
Solve the following system of linear inequalities bt graphing
x - y < 3
x + 2y > 6
Draw the first boundary line dotted:
x - y = 3
 The origin (0,0) as a test point satisfies x - y < 3, and so
we will shade the LEFT (upper) side of that line, since the origin is
on that side.
Draw the second boundary line dotted:
x + 2y = 6
The origin (0,0) as a test point satisfies x - y < 3, and so
we will shade the LEFT (upper) side of that line, since the origin is
on that side.
Draw the second boundary line dotted:
x + 2y = 6
 The origin (0,0) as a test point DOES NOT satisfy x + 2y > 6, and so
we will shade the RIGHT (upper) side of that green line, since the
origin is NOT on that side of the green line.
So we shad the region which is right of the green line and left of the
dark red line:
The origin (0,0) as a test point DOES NOT satisfy x + 2y > 6, and so
we will shade the RIGHT (upper) side of that green line, since the
origin is NOT on that side of the green line.
So we shad the region which is right of the green line and left of the
dark red line:
 (x-3)(sqrt(sin(7x)))/( sqrt( sin(7x) ) ),((6-x)/2)(sqrt(sin(7x)))/( sqrt( sin(7x) ) ) )}}}
Solve the system by addition.
5x - 4y = -5
x - 2y = -7
To make the y's cancel, multiply the bottom equation by -2,
then add vertically term by term:
5x - 4y = -5
-2x + 4y = 14
-------------
3x = 9
x = 3
To make the x's cancel, multiply the bottom equation by -5,
then add vertically term by term:
5x - 4y = -5
-5x + 10y = 35
--------------
6y = 30
y = 5
So the solution is (x,y) = (3,5)
That one could have been solved graphically:
(x-3)(sqrt(sin(7x)))/( sqrt( sin(7x) ) ),((6-x)/2)(sqrt(sin(7x)))/( sqrt( sin(7x) ) ) )}}}
Solve the system by addition.
5x - 4y = -5
x - 2y = -7
To make the y's cancel, multiply the bottom equation by -2,
then add vertically term by term:
5x - 4y = -5
-2x + 4y = 14
-------------
3x = 9
x = 3
To make the x's cancel, multiply the bottom equation by -5,
then add vertically term by term:
5x - 4y = -5
-5x + 10y = 35
--------------
6y = 30
y = 5
So the solution is (x,y) = (3,5)
That one could have been solved graphically:
 Then draw a horizontal line and a vertical line through the
point where the lines cross:
Then draw a horizontal line and a vertical line through the
point where the lines cross:
 and you see that the vertical line crosses the x-axis at 3,
and the horizontal line crosses the y-axis at 5. So we get
the same solution (x,y) = (3,5) by graphing that we get by
addition.
Edwin
and you see that the vertical line crosses the x-axis at 3,
and the horizontal line crosses the y-axis at 5. So we get
the same solution (x,y) = (3,5) by graphing that we get by
addition.
Edwin