Question 860794: Hi,
I am having a difficult time understanding probability. Can you please answer the following questions and provide me with simple instructions on how you achieved the answers. Thank you in advance
Five dice are rolled.
(a) Find the probability of getting all sixes. (Enter your answer as a fraction.)
(b) Find the probability of getting all the same outcomes. (Enter your answer as a fraction.)
(c) Find the probability of getting all different outcomes. (Enter your answer as a fraction.)
Answer by ben720(159)   (Show Source): (Show Source):
You can put this solution on YOUR website! A) When you roll the first die, there is a one in 6 probability of getting a 6. When you roll the second, there's another  chance. chance.
Because all of the numbers have to be 6, the chance all of them are 6's is
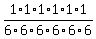
Because for every time you fail the first, which is a 5 in 6 chance, that entire tree of possibilities fails.

Because to multiply fractions, you multiply the denominators and numerators together.

Because 6^6 = 46656.
B) This part is very similar. The only difference is that you don't have to have the first roll in the calculations, as there's no chance you go wrong, as the first roll determines what the rest need to be. Therefore,

As 6^5 = 7776, the probability is 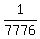
C) This part is different. As the first die cannot go wrong, as there's nothing before it to get the same as, this one is  . .
The next roll has a  chance as all the possibilities are open except for whatever the first die got. The third die has all the possibilities except whatever the first two dice got, therefore being chance as all the possibilities are open except for whatever the first die got. The third die has all the possibilities except whatever the first two dice got, therefore being 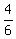 , and so on. , and so on.
Therefore the probability is 
|
|
|