SOLUTION: Compute P(x) using the binominal probability formula. Then determine whether the normal distribution can be used to estimate this probability. n=50, p=0.25, x=25

Algebra ->  Probability-and-statistics -> SOLUTION: Compute P(x) using the binominal probability formula. Then determine whether the normal distribution can be used to estimate this probability. n=50, p=0.25, x=25      Log On


   

Question 860660: Compute P(x) using the binominal probability formula. Then determine whether the normal distribution can be used to estimate this probability. n=50, p=0.25, x=25
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,

n=50, p=0.25, x=25

P+%2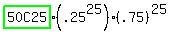8x%29=+highlight_green%28nCx%29%28p%5Ex%29%28q%29%5E%28n-x%29+ 

P(25) = highlight_green%2850C25%29%28.25%5E25%29%28.75%29%5E%2825%29+

126410606437752

P(25) = highlight_green%28126410606437752%29%28.25%5E25%29%28.75%29%5E25+ = .0000845

Note: We can use the normal distribution as a close approximation to the

 binomial distribution whenever n*p ≥ 5 and nq ≥ 5.

.25*50 = 12.5  and .75*50 = 37.5

Yes, We can use the normal distribution as a close approximation to the

 binomial distribution