Question 860181: VWXYZ is a rectangle-based pyramid where
WX = 66cm and XY = 32 cm. The vertex V is
vertically above the centre of the base.
Given that the slant heights VA and VB are
56 cm and 63 cm respectively, draw the net
of the pyramid and find its total surface
area. Also find the height and volume of
the pyramid.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! VWXYZ is a rectangle-based pyramid where
WX = 66cm and XY = 32 cm. The vertex V is
vertically above the centre of the base.
Given that the slant heights VA and VB are
56 cm and 63 cm respectively, draw the net
of the pyramid and find its total surface
area. Also find the height and volume of
the pyramid.
 Triangles WVZ and XYV have base 32 and altitude 63,
Each has area =
Triangles WVZ and XYV have base 32 and altitude 63,
Each has area =  (32)(63) = 1008 cm²
Both together have area 2004 cm²
Triangles YZV and XYV have base 66 and altitude 56,
Each has area = (32)(63) = 1008 cm²
Both together have area 2004 cm²
Triangles YZV and XYV have base 66 and altitude 56,
Each has area =  (66)(56) = 1848 cm²
Both together have area 3696 cm²
The rectangular base has area (66)(32) = 2112
So the entire surface area of the pyramid is
2004 cm² + 3696 cm² + 2112 cm² = 7812 cm²
-----------------------------------------------
When triangle WZV is folded upwards so that vertex V
is directly above O, then the right triangle OBV will
have base OB = 33, (half of 66) and hypotenuse BV = 63.
Using the Pythagorean theorem,
BV² = OB² + OV²
63² = 33² + OV²
3969 = 1089 + OV²
2880 = OV² (66)(56) = 1848 cm²
Both together have area 3696 cm²
The rectangular base has area (66)(32) = 2112
So the entire surface area of the pyramid is
2004 cm² + 3696 cm² + 2112 cm² = 7812 cm²
-----------------------------------------------
When triangle WZV is folded upwards so that vertex V
is directly above O, then the right triangle OBV will
have base OB = 33, (half of 66) and hypotenuse BV = 63.
Using the Pythagorean theorem,
BV² = OB² + OV²
63² = 33² + OV²
3969 = 1089 + OV²
2880 = OV²
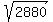 = OV = OV
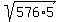 = OV = OV
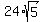 = OV, which is the height of the pyramid.
Checking, when triangle YZV is folded upwards so that
vertex V is directly above O, then the right triangle OAV will
have base OA = 16, (half of 32) and hypotenuse AV = 56.
Using the Pythagorean theorem,
AV² = OA² + OV² (That's OV when the sides are folded up)
56² = 16² + OV²
3136 = 256 + OV²
2880 = OV² = OV, which is the height of the pyramid.
Checking, when triangle YZV is folded upwards so that
vertex V is directly above O, then the right triangle OAV will
have base OA = 16, (half of 32) and hypotenuse AV = 56.
Using the Pythagorean theorem,
AV² = OA² + OV² (That's OV when the sides are folded up)
56² = 16² + OV²
3136 = 256 + OV²
2880 = OV²
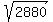 = OV = OV
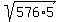 = OV = OV
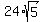 = OV, which gives the same height of the pyramid.
So that checks out.
Height of the pyramid = OV = = OV, which gives the same height of the pyramid.
So that checks out.
Height of the pyramid = OV = 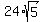 cm²
---------------------
The volume is calculated by the formula
V = cm²
---------------------
The volume is calculated by the formula
V = 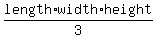 = = 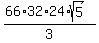 = = 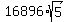 cm³.
Edwin cm³.
Edwin
|
|
|