Question 85996: This is a problem I have run into here at work. I need to solve for x in the following equation. Thanks for the help.
S=(1440*T)/(N*x*pi^2*D^2*acos((D-x)/D))
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! I assume that by 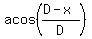 you mean you mean 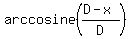 or ďthe angle whose cosine is or ďthe angle whose cosine is 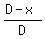 . .
.
Hereís some food for thought.
.
You have:
.

.
Letís begin by getting all the terms that contain x on the left side and everything
else on the right side. The first step is to multiply both sides by  . .
When you do, the equation becomes:
.

.
Next divide both sides by S and get:
.

.
Now, for reasons that will become apparent later, letís multiply both sides of this equation
by 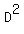 . .
.
This makes the equation become:
.

.
Now letís suppose we can force D to be some value other than zero (because if it were 0,
then 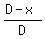 would involve a division by zero). Suppose for example we could make would involve a division by zero). Suppose for example we could make
D equal to x. If we could do this, then substituting x for D would make the equation become:
.

.
Notice two things: first  and second and second 
.
If you limit the angle to being between  and and  , then there are two possible , then there are two possible
values for this angle when D = x. Those values for  are are  and and 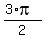 . .
.
Letís substitute  for for  . This changes the equation to: . This changes the equation to:
.

.
Next divide both sides of the equation by  or multiply by or multiply by 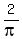 which leads to: which leads to:
.

.
And the right side multiplies out to:
.

.
Then you can solve for x by taking the cube root of both sides.
.
But donít forget that this requires that you be able to make D equal x.
.
And donít forget that you have another value possible because 
is also a possibility.
.
Letís now substitute 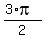 for for  . This changes the equation to: . This changes the equation to:
.

.
Next divide both sides of the equation by 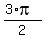 [or multiply both sides by [or multiply both sides by 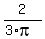 ] ]
which leads to:
.

.
And the right side multiplies out to:
.

.
Again, you can solve for x by taking the cube root of both sides.
.
You can do a similar analysis for  which implies that which implies that  which, which,
when solved for D, says that D must be set so that it equals  . So this leads to . So this leads to
replacing  with with 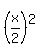 which is which is 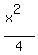 and replacing and replacing 
with the angle  because that is the only angle between because that is the only angle between  and and 
that has as its cosine the value -1. This leads to:
.

.
Next divide both sides of the equation by 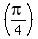 [or multiply both sides by [or multiply both sides by
 ] which leads to: ] which leads to:
.

.
And the right side multiplies out to:
.

.
Again, you can solve for x by taking the cube root of both sides.
.
I wonít belabor the point, but you can continue this analysis for other values. But it is
all based on the fact that to do this you must be able to control the value of D.
.
Like I said at the beginning, just food for thought. Hope the process stimulates you to find
something that you might be able to do to solve for x. Iíve done this rather rapidly,
so be sure to check the above to make sure that I didnít make some dumb math mistake Ö
which I often do unless Iím on my 4th cup of coffee Ö and Iím not at present.
.
|
|
|