Question 859829: Each side of the right triangle ABC is tangent to the circle with center o. The radius of the circle is 4 inches and the length AC is 12 inches. Find each of the following.
m∠C (Angle C)
m∠B (Angle B)
Line BC
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website! Each side of the right triangle ABC is tangent to the circle with center O. The radius of the circle is 4 inches and the length AC is 12 inches. Find each of the following.
m∠C (Angle C)
m∠B (Angle B)
Line BC

Draw radii (in green) to the three points of tangency,
OD, OE, and OF, which are perpendicular to the three
sides. Draw OC and OB. Extend FO till it intersects BC at G.
Then draw GH⊥AB

OD=4, so AF=4, and since AC=12, FC=8
∠FCO = ∠ECG because the center of inscribed circle O
is the intersection of the angle bisectors.
ΔCFO = ΔCEO hypotenuse and a side equal
∠FOC ≅ ∠EOC
∠FOE = 2∠FOC, CF = CE = 8
tan(∠FOC) =  = = 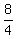 = 2 = 2
CE = CF = 8
tan(∠FOE) = tan(∠FOC) = 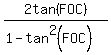 = = 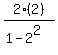 = = 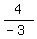 = = 
∠GOE = 180°-∠FOE
tan(∠GOE) = 180°-∠FOE
tan(∠GOE) = tan(180°-∠FOE) = -tan(∠FOE) = 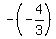 = = 
tan(∠GOE) = 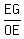 = = 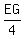
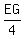 = = 
EG = 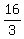
OG =  = = 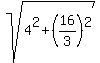 = = 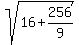 = =  = = 
ΔOEG ≅ ΔGHB because DE=GH=4 and ∠GBH = ∠OGE
parallel lines FG,AB cut by
transversal BC
GB = OG = 
BC = CE + EG + GB = 8 + 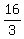 + +  = = 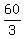 = 20 = 20
∠C = ∠ACB = cos-1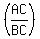 = cos-1 = cos-1 = cos-1 = cos-1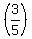 , approximately 53.13° , approximately 53.13°
∠B = ∠ABC = sin-1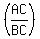 = sin-1 = sin-1 = sin-1 = sin-1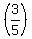 , approximately 36.87° , approximately 36.87°
Edwin
|
|
|