SOLUTION: Hi, I am working through my Application of derivatives assignment and I have found a lot of helpful information on this website, and I am now on my final question, and this is very

Algebra ->  Volume -> SOLUTION: Hi, I am working through my Application of derivatives assignment and I have found a lot of helpful information on this website, and I am now on my final question, and this is very      Log On


   

Question 858243: Hi, I am working through my Application of derivatives assignment and I have found a lot of helpful information on this website, and I am now on my final question, and this is very difficult for me since it is optimization and I really get confused with optimization, this is a two part question a) and b) that I am hoping anyone can provide me with help, as it would be much appreciated
A cardboard box with a square base is to have a volume of 8 litres.
(1 litre = 1000cm^3)
a) Find the dimensions that will minimize the amount of cardboard to be used. Define your domain.
b) The cardboard for the box costs 0.1 cents/cm^2 but the cardboard for the bottom is thicker, so it costs three times as much. Find the dimensions that will minimize the cost of the cardboard.

For part a) I understand to come up with a domain and an equation and then differentiate the equation to get the critical points which I will use to get the maximum and minimum values, but I am unsure how to do this at all
For part b) I understand that it is the same as part a) but this time you are involving the cost function as well, again, I am unsure of any of this
Any help would be highly appreciated
Thank You
Answer by josgarithmetic(39615) About Me  (Show Source):
You can put this solution on YOUR website!
x and x for the square bottom, and y for how tall.
yx%5E2=8%2Aliters%2A%281000%2Acm%5E3%2F%281%2Aliter%29%29
yx%5E2=8000, as cm^3.

Amount of cardboard would correspond to surface area of this box.
There are four sides and a top and bottom. The top and bottom are both square shaped:
A for area,
A=4xy%2B2x%5E2.
-
A couple ways to go from there. Substitute for x or substitute for y. Try y=8000%2Fx%5E2, from the volume, and use in the AREA equation.

A=4x%288000%2Fx%5E2%29%2B2x%5E2
highlight_green%28A=24000%2Fx%2B2x%5E2%29.

Wanting to minimize A, you want 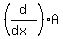%28d%2F%28dx%29%29A, and set equal to zero, and solve for the value of x that you need; and then determine what is y.
Derivative of A, %28d%2F%28dx%29%29%2824000x%5E-1%2B2x%5E2%29
-24000x%5E-2%2B4x%5E1
4x-24000%2Fx%5E2=0
4%28x-8000%2Fx%5E2%29=0 the 4 obviously not being zero.
x-8000%2Fx%5E2=0
x%2A%28x%5E2%29%2F%28x%5E2%29-8000%2Fx%5E2=0
%28x%5E3-8000%29%2F%28x%5E2%29=0
-
The focus is on the NUMERATOR being zero;
x%5E3-8000=0
x%5E3=8000
x=root%283%2C8000%29
x=2%2A10
highlight%28x=20%29.
-
Now the value for y can be found.
y=8000%2Fx%5E2
y=8000%2F%2820%2A20%29
y=8000%2F400
highlight%28y=20%29, which should seem to make sense.

I have not done the part (b); only did part (a). You could start this using 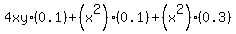4xy%2A%280.1%29%2B%28x%5E2%29%2A%280.1%29%2B%28x%5E2%29%2A%280.3%29 for the cost, needing some simplification and other treatment. Maybe with the part been done, you may find a way to accomplish part b?