Question 858186: How do you find the domain and range of the rational function: 5x^2+5/x^2+6x+9. Already found the asymptotes and x and y intercepts.
Vertical Asymptotes: x=-3
Horizontal Asymptotes: y=5
y-int.: (0,5/9)
x-int.: Does Not Exist
Use a graphing device to confirm your answer. (Use interval notation).
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! domain: all the real numbers except 
range: [ , , ) but I do not know how you would know. ) but I do not know how you would know.
Are you in a calculus class?
Are you studying derivatives?
We know that  is always positive, is always positive,
and that its value approaches  at both ends, at both ends,
but how low can it go?
Maybe you are supposed to calculate the derivative and find the minimum.
Maybe you are supposed to figure out the minimum some other way.
Apparently you are expected to use some graphing software to confirm.
WITHOUT DERIVATIVES:
If  has a minimum has a minimum  , ,
 has a single solution. has a single solution.


so  <--> <--> has a single solution. has a single solution.
That means the discriminant of that quadratic equation is zero.






 The minimum of The minimum of  is is  . .
WITH DERIVATIVE:

and find out that the derivative is
undefined for  , ,
negative for 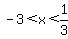 , ,
positive for 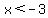 and and 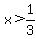 , ,
and zero for  , ,
indicating a minimum of the function for  . .
Then, the minimum value for the function is
From that I know that for very negative values  is barely above is barely above  . .
As  increases, increases,
 grows without bounds as grows without bounds as  approaches approaches  . .
After that,
 decreases to its decreases to its  minimum for minimum for  , ,
and then  increases again towards increases again towards  . .
Seeing all that in a graph requires viewing a bird's eye view and a zoomed-in view:
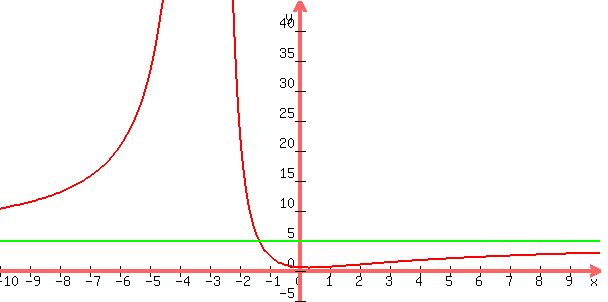 
|
|
|