Question 857886: In a sequence of 6 numbers every number after the first two is the average of the previous two numbers
The fourth number in the sequence is 22 and the 6th number is 45.
Determine all six numbers in the sequence.
Answer by JulietG(1812)   (Show Source): (Show Source):
You can put this solution on YOUR website! We can immediately tell that the equation for the fifth number (E) is:
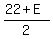 =45 =45
Therefore, E + 22 = 90; E = 68
Our sequence looks like this:
A, B, C, 22, 68, 45
Let's work backward to find C.
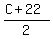 = 68 = 68
C + 22 = 136
C = 114
Now we have:
A, B, 114, 22, 68, 45
22 is the average of 114 and B.
44 = 114 + ?
B = -70
Now we have:
A, -70, 114, 22, 68, 45
What is A?
A + (-70) = 114*2, or 228
A = 298
Sequence is:
298, -70, 114, 22, 68, 45
.
Let make sure that works.
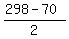 =114 =114
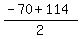 =22 =22
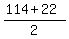 =68 =68
 =45 =45
Success!
|
|
|