Question 857848: Find the vertices and foci of the illipse given by the equation 4x^2 + 9y^2 = 144
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you know basic algebra and learn the meaning of "ellipse" and related words, such as "vertices", "foci", and "major axis", you know all you need to know about ellipses.
Looking at  <--> <--> <--> <--> , ,
you notice the following:
1) The ellipse is symmetrical with respect to the x- and y-axes (which means its center is (0,0), the origin).
You know that because if the coordinates of a point (p,q) satisfy the equation,
so will the coordinates of the symmetrical points (p,-q) and (-p,q).
2) When  , the first term is zero, and you get the most extreme values of , the first term is zero, and you get the most extreme values of  , ,
 . .
Those are the coordinates of the highest and lowest points on the ellipse,
(0,4) and (0,-4).
They are the ends of the vertical axis of symmetry,
at a distance of  units from the center. units from the center.
3) When  , the first term is zero, and you get the most extreme values of , the first term is zero, and you get the most extreme values of  , ,
 . .
Those are the coordinates of the most extreme left and right points on the ellipse,
(6,0) and (-6,0), at a distance of  units from the center.. units from the center..
Since they are the axis ends at the greatest distance (because  ), ),
they are the ends of the major axis,
and are called vertices.
Their distance from the center is the semi-major axis  . .
The points (0,4) and (0,-4) are the ends of the minor axis
(sometimes called co-vertices),
and their distance to the center is the semi-minor axis,  . .
The foci are on the major axis (with  , as the center and vertices), , as the center and vertices),
and their distance to the center,  , can be calculated from the formula , can be calculated from the formula
 . .
In this case,
 --> --> --> --> --> -->
So  --> --> --> --> . .
That means that for the foci,  . .
The foci are at 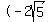 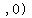 and and   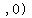 . .
|
|
|