|
Question 856598: Find the smallest natural number that can be expressed as the sum of the squares of two, not necessarily distinct, natural numbers in two different ways.
Show all work!
Thank you!
-Lulu
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! My answer is  , but my work is not that elegant. , but my work is not that elegant.
I would post the problem in the forum of the artofproblemsolving website,
and then try to understand the very brief and elegant answer obtained there.
A pair of natural numbers  and and  (not necessarily different from each other, maybe (not necessarily different from each other, maybe  ) squared ad up to ) squared ad up to  . .
A different pair of natural numbers  and and  (not necessarily different from each other) squared ad up to (not necessarily different from each other) squared ad up to  . .
One way would be making a table with
values for  (from 1 to 10) in the first column, (from 1 to 10) in the first column,
values for  (from 1 to 10) in the first row, (from 1 to 10) in the first row,
and the sum of squares  where column where column  meets row meets row  . .
Comparing each values on each row, to other values
on the rows below, we would find many matching sums of squares of the same pair of numbers.
They are symmetrically arranged to either side of the diagonal.
We would be looking for matches between sums of squares of different pairs of numbers,
like  matching matching  , ,
and  matching matching  . .
Another approach:
 --> --> --> -->
So we need an integer that can be written as two different products,
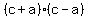 and and 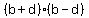 . .
 would lead you to solve systems like would lead you to solve systems like
 --> --> and and
 --> -->
to get 
|
|
|
| |