The number of ways to arrange the 25 things where "AB"
is one thing, and the other letters are the other 24 things, is:
{AB,C,D,E,F,...,X,Y,Z} is 25!
The number of ways to arrange the 25 things where "BA"
is one thing, and the other letters are the other 24 things, is:
{BA,C,D,E,F,...,X,Y,Z} is also 25!
So that 2×25!
out of the number of ways to arrange the 26 things:
{A,B,C,D,E,F,...,X,Y,Z}
which is 26!
Answer: 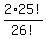 =
= 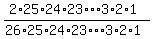 =
= 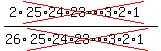 =
= 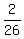 =
=  Edwin
Edwin