|
Question 856008: how can you find the domain and range of y=-3/4(x-1/2)^2+9 ?
Found 2 solutions by KMST, josgarithmetic:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! It is a quadratic function.
As for all polynomial functions,
its domain is all the real numbers.
Because it is a quadratic function
(one of those that graph as parabolas),
its range is more limited.
Quadratic functions have a minimum (if the coefficient of the term with  is positive),
or a maximum (when that coefficient is negative).
In this case the coefficient,  , is negative, and there is a maximum.
You do not need to know anything about quadratic functions to know that the square of a number is at least zero (if that number is zero), and often positive, but never negative.
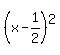 is positive or at least zero:  .
So,  is negative or at most zero:  .
As a consequence,   is at most  :
The range includes only 9 and all real numbers that are less than 9.
Some would write is as ( ,].
Others may prefer a different notation, such as {x |  }
Answer by josgarithmetic(39620)  (Show Source):
You can put this solution on YOUR website! Parabola in standard form. y as a function of , so axis of symmetry is parallel to the y axis.
DOMAIN: all real numbers.
RANGE: Coefficient is negative on the term and the vertex is therefore a maximum, at (1/2, 9). Now, range?
|
|
|
| |
