SOLUTION: 2 isosceles triangles have legs that are 26 and areas that are equal. If the base of one triangle is 48. Find the base of the other triangle ? *i know that in an isosceles triangl

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: 2 isosceles triangles have legs that are 26 and areas that are equal. If the base of one triangle is 48. Find the base of the other triangle ? *i know that in an isosceles triangl      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 855917: 2 isosceles triangles have legs that are 26 and areas that are equal. If the base of one triangle is 48. Find the base of the other triangle ?
*i know that in an isosceles triangle the sides that are connected to the vertex angle is congruent and the base angles are also congruent* i have tried using the Pythagorean theorem but its not working*(Pythagorean theorem= a^2+b^2=C^2
please do help me and thank you
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,

Perhaps this picture will help: 

the 'h' is a 'leg', other leg = 24 (h bisects the base)

hypotenuse = 26



line segment of Height to the base bisects the base (base = 48)

Therefore: 26^2 - 24^2 = h^2 = 100, h = 10

 A = 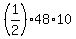%281%2F2%2948%2A10 = 240

 Find the base of the other triangle 

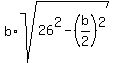
 A = 240 = %281%2F2%29b%2Asqrt%2826%5E2+-+%28b%2F2%29%5E2%29

    480= b%2Asqrt%2826%5E2+-+%28b%2F2%29%5E2%29

    480^2/b^2 = 26^2 - (b^2/4

    b^4  -4(26^2)b^2 + 4(480^2)  Let x = b^2

    x^2 - 2704x + - 921600

x = 400 0r x = 2304

 b = 20  0r b = 48

the base of the other triangle is 20

CHECKING our answer***

 26^2 -10^2 = 576= h^2,   h = 24   AND  A+=+%281%2F2%2920%2A24+=+240

Wish You the Best in your Studies.