Question 855786: I am having difficulty with this question and was wondering if you could give me a hand
Five numbers have a median of 7, a mode of 9, a range of 5 and a mean of 7 what are the 5 numbers?
cheers
Found 2 solutions by rothauserc, KMST:
Answer by rothauserc(4718)   (Show Source):
You can put this solution on YOUR website! let a, b, c, d, e be the five numbers
we know that c is 7 since the median is 7
the mean is 7 so (a + b + 7 + d + e) / 5 = 7
the range is 5 so we have e - a = 5
mode is 9 so we know that there is more than one 9
we have a, b, 7, 9, 9
e - a = 5 so a is 4
4, b, 7, 9, 9 we need to solve for b
4+b+7+9+9 = 35 (from definition of the mean)
b = 35 - 29 = 6
therefore our 5 numbers are
4, 6, 7, 9, 9
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! Mode is the most repeated value, so two of the numbers must be
 and .
The median is a value such that as many of the numbers are lesser than the median as are greater than the median.
With five numbers, because 5 is odd, the median has to be one of the numbers,
so  is one of the numbers,
and since two of the numbers are 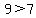 the other two numbers must be less than  .
The range is the difference between the greatest and the least of the numbers.
The range is  the greatest of the numbers is  ,
so the least of the numbers is  .
Knowing for of the numbers, and the mean 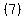 of the five numbers,
the fifth number, which I will call  , can be found from the definition of mean:
 .
The five numbers are:
 ,  , , and .
|
|
|
