Question 855643: The perimeter of two similar triangles have a ratio of 2:4. The sum of the areas of the triangles add up to 100cm^2. What is the area of each triangle?
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Perimeter being a length, or a distance, means the side lengths are also in the same 2:4 proportion, actually 1:2 ratio, because 1:2 is reduced.
Small triangle:
perimeter x+y+z, and if assumed z is a hypotenuse and the triangles are Right, then
area is  .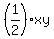
Large triangle:
perimeter would be 2x+2y+2z=2(x+y+z). As similar to the small one,
area is  .
Look at now the ratio of their areas. (1/2):2, or  , small to large; This means, if cut the large AND small together into 5 equal parts, the small triangle is 1 of those parts, and the large triangle is 4 of those parts; together making the 5 equal parts.
Cut  into 5 equal parts:  in each part. This means small triangle is and large triangle is  .
|
|
|
