SOLUTION: Determine the end behavior, zeros, and multiplicity of each zero a) 30x^4-2x^5 b) 0.01(x-20)^2(x+4)^4(x-5)(x+12)^3(x-10)

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Determine the end behavior, zeros, and multiplicity of each zero a) 30x^4-2x^5 b) 0.01(x-20)^2(x+4)^4(x-5)(x+12)^3(x-10)      Log On


   

Question 855635: Determine the end behavior, zeros, and multiplicity of each zero
a) 30x^4-2x^5
b) 0.01(x-20)^2(x+4)^4(x-5)(x+12)^3(x-10)
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
This is help for number "b".

Degree is 11. The coefficient on the leading term, 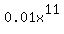0.01x%5E11, will be positive. As x becomes unbounded to the left, the polynomial's value decreases; and as x becomes unbounded to the right, the polynomial's value increases; since the degree of the polynomial is odd and the leading coefficient is positive.

The exponent on each variable factor gives you the multiplicity of the zero directly. The polynomial (which is actually in its factored form) has five zeros. Those zeros: 20, -4, 5, -12, 10.