Question 855004: i am helping my daughter with her homework and we are both stumped...she got to the last question...i think i know the answer and she doesnt but i dont now how i know...just a guess and would like to review with her the process...Here we go the length of a rectangular area rug is given by the trinomial c^2 - 8c -48 and length is(c-12) find the width...she has tried several ways and none make sense...please help us... i will review with her...need the steps...i think it is c-4 but dont know how to get it...she thinks she needs to factor the trinomial
This is our first time using...great site
Thanks in advance
Found 2 solutions by richwmiller, josgarithmetic:
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! if c^2 - 8c -48 is the area
(c-12) is one factor (length) and (c+4) is the other (width)
We don't know the value of c
let's foil to get the trinomial
(c-12)*(c+4)
F- c^2
O- 4c
I- -12c
L- -12*4=-48
add them
c^2 - 8c -48
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Factoring the trinomial could help ---- IF it is factorabale.
Area is Length multiplied by Width. You already seem to understand that.
Abbreviating with your variables,
 and you have and you have  ; and you want w. I am using w as width. ; and you want w. I am using w as width.
Using formula for area knowledge,  . Further using your variable expressions,... . Further using your variable expressions,...
 . .
Is the trinomial easily factorable? IS it factorable?
-
Let us try to factor the trinomial for the area:
We want two numbers so that their sum is  and their product is and their product is  . What combinations can we try? . What combinations can we try?
-
48=12*4, MAYBE this will work (there are other combinations).
(c__12)(c__4)=... we do not yet know the signs.
12*4=48, but we want NEGATIVE 48.
12c and 4c can give 8c, but which sign to which in each binomial?.
 ... NOT what we want, but we are near. ... NOT what we want, but we are near.
-
Trying the signs the other way:
 ----That is what we want. ----That is what we want.
You can now identify the width expression, w, directly from the multiplication there. The area is the trinomial product way on the right hand side. The far left hand side shows the length c-12, multiplied by the width, c+4.
ANSWER: The width, w, is  . .
ADDITIONALLY, you can actually try  , using polynomial division, which is really no trouble here, and will give the same result as found. That means, divide the area , using polynomial division, which is really no trouble here, and will give the same result as found. That means, divide the area  , by the length , by the length 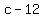 . The quotient will be . The quotient will be 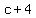 . .
|
|
|