|
Question 854950: The sum of 6 consecutive even numbers is 366. What is the third number in this sequence?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If  = the third number, the numbers are = the third number, the numbers are
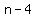 , , 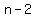 , ,  , ,  , , 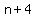 , and , and 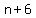 . .
Their sum is
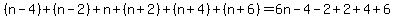





NOTES:
1) The teacher may expect some talk about arithmetic sequences, but it is easy enough as done above.
2) As mental math (as I would do for a multiple choice test),
I know that the sum of consecutive terms in an arithmetic sequence is the average times the number of terms. That average would be  . I also know that in an arithmetic sequence the average is the median, and with 6 terms that median would be halfway between the third and fourth terms, so the third and fourth terms should be 60 and 62. . I also know that in an arithmetic sequence the average is the median, and with 6 terms that median would be halfway between the third and fourth terms, so the third and fourth terms should be 60 and 62.
3) If I read "consecutive even numbers" or "consecutive odd numbers", I simply call some convenient number  (not caring if (not caring if  is odd or even until the end). I just make the consecutive even or odd numbers 2 units apart from one another. At the end, the results should be even or odd as required, or else the problem has no answer (or I made a mistake). is odd or even until the end). I just make the consecutive even or odd numbers 2 units apart from one another. At the end, the results should be even or odd as required, or else the problem has no answer (or I made a mistake).
|
|
|
| |