SOLUTION: Find the vertices, foci, and center of the hyperbola. Graph the equation. 4y^2 - x^2 - 2x - 16y + 11 = 0

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Find the vertices, foci, and center of the hyperbola. Graph the equation. 4y^2 - x^2 - 2x - 16y + 11 = 0      Log On


   

Question 854643: Find the vertices, foci, and center of the hyperbola. Graph the equation.
4y^2 - x^2 - 2x - 16y + 11 = 0
Answer by lwsshak3(11628) About Me  (Show Source):
You can put this solution on YOUR website!
Find the vertices, foci, and center of the hyperbola. Graph the equation.
4y^2 - x^2 - 2x - 16y + 11 = 0
4y^2-16y -x^2-2x=-11
complete the square:
4(y^2-4y+4) -(x^2+2x+1)=-11+16-1
4(y-2)^2-(x+1)^2=4
%28y-2%29%5E2-%28x%2B1%29%5E2%2F4=1
This is an equation of a hyperbola with vertical transverse axis.
Its standard form of equation: 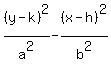%28y-k%29%5E2%2Fa%5E2-%28x-h%29%5E2%2Fb%5E2, (h,k)=coordinates of center
For given hyperbola:
center: (-1,2)
a^2=1
a=1
vertices: (-1,2±a)=(-1,2±1)=(-1,1) and (-1,3)
b^2=4
b=2
c^2=a^2+b^2=1+4=5
c=√5≈2.2
foci: (-1,2±c)=(-1,2±2.2)=(-1,-.2) and (-1,4.2)
see graph below:
y=(1+(x+1)^2/4)^.5+2