Question 854623: What is the smallest positive integer that,
when multiplied by 7, yields a product
in which all of the digits are 5ís?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I see that as a problem involving modular arithmetic, but I am not sure of what language/jargon to use, so I will try to use terms we both understand the same way.
If  then then  must be a multiple of 7. must be a multiple of 7.
We must find a  that is a multiple of 7. that is a multiple of 7.
 , ,  , ,  , , 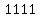 and and 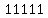 are not, are not,
but  so so

which shows that  is the smallest positive integer that, is the smallest positive integer that,
when multiplied by 7, yields a product in which all of the digits are 5ís.
NOTE 1: The number is easy to find with a calculator, but is is easy enough without one.
Without a calculator, you can figure out the remainders of dividing by 7
1, 10, 100, 1000, and so on.
The first ones are 1, 3, 2, 6, 4, and 5.
So the remainder of dividing by 7
 is is  ; ;
the remainder of dividing by 7
 is is  ; ;
the remainder of dividing by 7
 is is  , ,
which differs by a multiple of 7 from  , and so on. , and so on.
The remainder of dividing by 7

differs by a multiple of 7 from
 , ,
meaning that 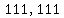 is a multiple of 7. is a multiple of 7.
NOTE 2:
This is the kind of question I would ask in a forum at the artofproblemsolving website.
There you are likely to find a middle school student who could answer the question.
|
|
|