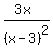You must include a term with a denominator
which is a lower power of a denominator.
So since (x-3)² is to the 2nd power, you must
include a term with the lower power (x-3) in
the denominator.
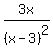
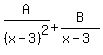Notice also that even though (x-3)² is degree 2 if
multiplied out, we do not need "Ax+B" for its
numerator because it is factored as the power of
only a first degree binomial.
Clear of fractions:
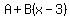
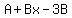Since the sides must be identical, we can
equate the like terms on both sides:
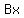So B = 3
There are no constant terms on the left, so put 0
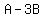Substitute 3 for B
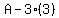
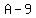
So
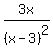
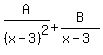becomes
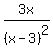
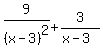Edwin
