|
Question 854423: Please factorize the following
15x2 -2x -1
and
a3 +6a2b +12ab3 +8b3
thank you
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 

(I know you wrote 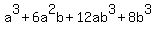 , but I think there was a typo somewhere). , but I think there was a typo somewhere).
How did I get it?
The factorization of

is easier to calculate this way:
If  <--> <--> , ,

If that is Greek to you, there is another, more traditional way.
To factorize something like  , you multiply the coefficients at the ends , you multiply the coefficients at the ends
(in this case, 15 and -1, that multiply to give -15),
and look for pairs of factors of that result that will add to the middle coefficient (-2 in this case).
When you figure out that 3 and -5 are those factors,
you re-write the polynomial with two middle terms with those coefficients,
that is  and and 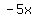 in place of the middle term in place of the middle term  , ,
and then you factorize by grouping:

With 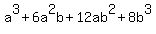 it is a question of realizing that it is a question of realizing that
 is the cube of is the cube of  and and
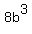 is the cube of is the cube of 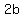 . .
That should make you suspect that it could be the cube of a binomial:

If you do the indicated operations,
 and and  , ,
and you find that indeed 
|
|
|
| |