SOLUTION: I really need help with this one, can someone please help me Use coordinate geometry to prove that the quadrilateral OPQR with vertices O(0,0),P(9,3),Q(9,8), and R(-3,4) is an i

Algebra ->  Length-and-distance -> SOLUTION: I really need help with this one, can someone please help me Use coordinate geometry to prove that the quadrilateral OPQR with vertices O(0,0),P(9,3),Q(9,8), and R(-3,4) is an i      Log On


   

Question 85404: I really need help with this one, can someone please help me
Use coordinate geometry to prove that the quadrilateral OPQR with vertices O(0,0),P(9,3),Q(9,8), and R(-3,4) is an isosceles trapezoid.
Found 2 solutions by scianci, Edwin McCravy:
Answer by scianci(186) About Me  (Show Source):
You can put this solution on YOUR website!
Consider the lengths of the 4 sides:
OP = sqrt%28%280+-+9%29%5E2+%2B+%280+-+3%29%5E2%29
= sqrt%28%28-9%29%5E2+%2B+%28-3%29%5E2%29
= sqrt%2881+%2B+9%29
= sqrt%2890%29
PQ = sqrt%28%289+-+9%29%5E2+%2B+%283+-+8%29%5E2%29
= sqrt%28%280%29%5E2+%2B+%28-5%29%5E2%29
= sqrt%280+%2B+25%29
= sqrt%2825%29
= 5
QR = sqrt%28%289+-+%28-3%29%29%5E2+%2B+%288+-+4%29%5E2%29
= sqrt%2812%5E2+%2B+4%5E2%29
= sqrt%28144+%2B+16%29
= sqrt%28160%29
RO = sqrt%28%28%28-3%29+-+0%29%5E2+%2B+%284+-+0%29%5E2%29
= sqrt%28%28-3%29%5E2+%2B+4%5E2%29
= sqrt%289+%2B+16%29
= sqrt%2825%29
= 5
Since PQ = RO, this proves that it's isosceles. To prove that it's a trapezoid, consider the slope of each side:
slope OP = %280+-+9%29%2F%280+-+3%29
= -9/-3 = 3
slope PQ = %289+-+9%29%2F%283+-+8%29
= 0/-5 = 0
slope QR = %289+-+%28-3%29%29%2F%288+-+4%29
= 12/4 = 3
slope RO = %280+-+%28-3%29%29%2F%280+-+4%29
= 3/-4 = -3/4
Since OP and QR have equal slopes, they are parallel. Furthermore, since they are the only sides that are parallel, by definition that makes the quadrilateral a trapezoid.

Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
I really need help with this one, can someone please help me
Use coordinate geometry to prove that the quadrilateral OPQR
with vertices O(0,0),P(9,3),Q(9,8), and R(-3,4) is an isosceles
trapezoid.





We have to show that OP II QR, i.e., that both
have the same slope. 

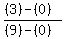mOP = %28+%283%29-%280%29%29%2F%28%289%29-%280%29%29 = 3%2F9 = 1%2F3

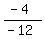mQR = %28+%284%29-%288%29%29%2F%28%28-3%29-%289%29%29 = %28-4%29%2F%28-12%29 = 1%2F3

Their slopes are equal, so OPQR is either a trapezoid or a parallelogram.

Now let's show that PQ = RO

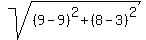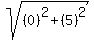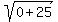DPQ = sqrt%28%289-9%29%5E2+%2B+%288-3%29%5E2%29 = sqrt%28%280%29%5E2+%2B+%285%29%5E2%29 =sqrt%280+%2B+25%29 = sqrt%2825%29 = 5 

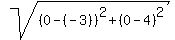DRO = sqrt%28%280-%28-3%29%29%5E2+%2B+%280-4%29%5E2%29 = sqrt%28%283%29%5E2+%2B+%28-4%29%5E2%29 = sqrt%289+%2B+16%29 = sqrt%2825%29 = 5

You might think this is enough to show that that OPQR is an isosceles
trapezoid since one pair of opposite sides are parallel and the other 
pair of opposite sides are equal in length.

However, that could be said about a rectangle.  We must rule out
a rectangle. (Yes we can look and see that it's not a rectangle,
but "looking and seeing" is not acceptable. The easiest way to do 
this is to rule out a right angle using slopes. We will show that
OP is not perpendicular to RO

We have already found the slope of OP as 1/3. So we will rule out
OPQR as being a rectangle by showing that the slope of RO is not
the "negative reciprocal" of 1/3.  That is to show that the slope of
RO is not -3.

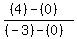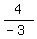mRO = %28+%284%29-%280%29%29%2F%28%28-3%29-%280%29%29 = 4%2F%28-3%29 = -4%2F3

-4%2F3 is not equal to -3 so we have ruled out a rectangle.

So OPQR must be an isosceles trapezoid.

Edwin