Question 852838: find the rectangle coordinates of the polar point -5, 5pi/2
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the rectangle coordinates of the polar point (r, ) = (-5, ) = (-5,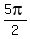 ) )
This one is better done graphically than algebraically:
To plot the polar point (r, ), start at the rectangular point
(0,r). Think of a radius drawn from the origin to that point on the x-
axis. That's the green line on the graph below connecting the origin
to the rectangular point (x,y) = (-5,0)
That is, we start with a radius r = x = -5 on the x-axis at the rectangular
point (-5,0) like this: ), start at the rectangular point
(0,r). Think of a radius drawn from the origin to that point on the x-
axis. That's the green line on the graph below connecting the origin
to the rectangular point (x,y) = (-5,0)
That is, we start with a radius r = x = -5 on the x-axis at the rectangular
point (-5,0) like this:

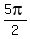 is is 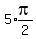 which means it is 5 right angles,
or 5 90-degree angles.
So we swing the green line counter-clockwise through the
angle which means it is 5 right angles,
or 5 90-degree angles.
So we swing the green line counter-clockwise through the
angle 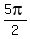 (five 90° angles, or (five 90° angles, or 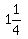 revolutions,
indicated by the curved red line below: revolutions,
indicated by the curved red line below:
 So the green radius ended up with its tip at the rectangular point (0,-5).
So the polar point (r,
So the green radius ended up with its tip at the rectangular point (0,-5).
So the polar point (r, ) = (-5, ) = (-5,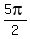 ) is the exact same
point as the rectangular point (x,y) = (0,-5).
Edwin ) is the exact same
point as the rectangular point (x,y) = (0,-5).
Edwin
|
|
|