Question 85221: If f(x) = x(x – 1)(x – 4)2, use interval notation to give all values of x
where f(x) > 0.
a. (–∞, 0) ∪ (4, ∞)
b . (–∞, 1) ∪ (4, ∞)
c . (0, 1) ∪ (4, ∞)
d . (–∞, 0) ∪ (1, 4) ∪ (4, ∞)
I believe the answer is (–∞, 0) ∪ (4, ∞). Can someone please let me know if I'm right?
thanks
Answer by scianci(186)   (Show Source):
You can put this solution on YOUR website! First, find the critical values. This is easy since your f'(x) is in factored form. The critical values are 0 , 1 and 4. This creates 4 intervals within the set of real numbers: (-inf., 0) , (0 , 1) , (1 , 4) and (4 , inf.) Test the sign of f'(x) in each of these intervals. Use -1 , 1/2 , 2 and 5 as test values. Plug each of these into the factored expression for x and analyze whether ea. factor is pos. or neg. for that particular value of x. If the number of neg. factors is even, the expression's value is pos. If the number of neg. factors is odd, the expression's value is neg. Bear in mind that the 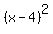 factor will always be pos.:
f'(-1) is pos. [2 neg. factors]
f'(1/2) is neg. [1 neg. factor]
f'(2) is pos. [0 neg. factors]
f'(5) is pos. [0 neg. factors]
The answer is d.
|
|
|
