SOLUTION: Two fair dice are rolled. Given that the dice land on different numbers, what is the probability that at least one land on 3.

Algebra ->  Probability-and-statistics -> SOLUTION: Two fair dice are rolled. Given that the dice land on different numbers, what is the probability that at least one land on 3.      Log On


   

Question 852150: Two fair dice are rolled. Given that the dice land on different numbers, what is the probability that at least one land on 3.
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!

Here are all 36 possible dice rolls:

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6) 

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6) 

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6) 

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6) 

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) 

--------------------------------------------------------

Since we are given that the dice land on different numbers,
we reduce the sample space by eliminating all the cases 
where the numbers are the same, so we only have this
reduced sample space of 30 dice rolls.

--------------------------------------------------------

      (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1)       (2,3) (2,4) (2,5) (2,6) 

(3,1) (3,2)       (3,4) (3,5) (3,6) 

(4,1) (4,2) (4,3)       (4,5) (4,6) 

(5,1) (5,2) (5,3) (5,4)       (5,6) 

(6,1) (6,2) (6,3) (6,4) (6,5) 

-------------------------------------------------

Now we'll color all the 3's red

-------------------------------------------------

      (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1)       (2,3) (2,4) (2,5) (2,6) 

(3,1) (3,2)       (3,4) (3,5) (3,6) 

(4,1) (4,2) (4,3)       (4,5) (4,6) 

(5,1) (5,2) (5,3) (5,4)       (5,6) 

(6,1) (6,2) (6,3) (6,4) (6,5) 

------------------------------------------------

Now count the red threes.  I count 10.  Did I color all the 3's red?
So that's 10 out of 30.  "Out of" means "over" so the probability is
10 over 30 or 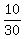10%2F30 or 1%2F3.

Edwin