SOLUTION: If the probability of a tennis player serving an ace is 1/6, what's the probability that the player will serve 3 aces out of 8 serves? I know it's independent probability. I did

Algebra ->  Probability-and-statistics -> SOLUTION: If the probability of a tennis player serving an ace is 1/6, what's the probability that the player will serve 3 aces out of 8 serves? I know it's independent probability. I did      Log On


   

Question 852124: If the probability of a tennis player serving an ace is 1/6, what's the probability that the player will serve 3 aces out of 8 serves?
I know it's independent probability. I did it like this:
for "non-ace" results, the prob. is 5/6
for 8 serves, the prob of 3 aces is:
1/6 * 1/6 * 1/6 * 5/6 * 5/6 * 5/6 * 5/6 * 5/6 = 3125/1,679,616 = approx. 0.00186, or 0.186%, or 186/1000.
Am I even close?
Found 3 solutions by Fombitz, ewatrrr, Theo:
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
Yes and no.
I think you've got the concepts but you're missing a lot of terms.
Since you don't know when the ace is served, the example you gave is only one possible outcome.
It could have been
AAANNNNN
or
ANAANNNN
or
NNNNNAAA
So you need to capture all of the possible outcomes that each individually have a probability of 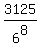3125%2F6%5E8
You can use Pascal's triangle with 9 terms (1,8,28,56,70,56,28,8,1).
So for no aces, there is 1 term (NNNNNNNN)
For 1 ace, 8 terms (ANNNNNNN, NANNNNNN, .... , NNNNNNNA)
For 2 aces, 28 terms (too many terms to write out)
For 3 aces, 56 terms.
So then,
highlight%28P%283%29=56%2A%281%2F6%29%5E3%2A%285%2F6%29%5E5=0.10419%29
The other terms are,
P%280%29=1%2A%281%2F6%29%5E0%2A%285%2F6%29%5E8=0.23257
P%281%29=8%2A%281%2F6%29%5E1%2A%285%2F6%29%5E7=0.37211
P%282%29=28%2A%281%2F6%29%5E2%2A%285%2F6%29%5E6=0.26048
P%284%29=70%2A%281%2F6%29%5E4%2A%285%2F6%29%5E4=0.02605
P%285%29=56%2A%281%2F6%29%5E5%2A%285%2F6%29%5E3=0.00417
P%286%29=28%2A%281%2F6%29%5E6%2A%285%2F6%29%5E2=0.00042
P%287%29=8%2A%281%2F6%29%5E7%2A%285%2F6%29%5E1+=0.000024
P%288%29=1%2A%281%2F6%29%5E8%2A%285%2F6%29%5E0+=0.0000006
If you add all the terms, they do sum to 1.

Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,

Note: The probability of x successes in n trials is: 

P (x)= nCx+%28p%5Ex%29%28q%29%5E%28n-x%29  where p and q are the probabilities of success and failure respectively. 

In this case p = 1/6 & q = 5/6  n = 8

 = %28n%21%29%2Fx%21%28n+-+x%29%21+=+8%2A7%2A6%2F%282%2A3%29+=+56 

P(x=3) =+56%281%2F6%29%5E3%285%2F6%29%5E5+=+.1042  You had just not used the 'combination factor' of 56

Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
close but no cigar.
if you multiply that by the number of possible ways you can get 3 things out of 8 things, then you would be right.
this, i believe, is a binomial probability type problem.
the formula for binomial probability is:
p(x) = nCx * p^x * q^(n-x)
in your problem:
n = 8
x = 3
n-x = 5
p = (1/6)
q = (5/6)
using these values, the formula becomes:
p(3) = 8C3 * (1/6)^3 * (5/6)^5
8C3 is equal to (8*7*6) / (1*2*3) which is equal to 56.
(1/6)^3 is equal to .004630
(5/6)^5 is equal to .401878
.004630 * .401878 is equal to .001860
formula becomes:
p(3) = 56 * .004630 * .401878 which is equal to 56 * .001860 which is equal to .104199

you were close.
you calculated correctly for one of the possible ways you can get 3 aces out of 8 serves.
there were 55 more ways to do that.
i'll just list the first 3 so you can see what i mean.
let a = probability to get an ace which is equal to 1/6
let b = probability to not get an ace which is equal to 5/6.
you showed one way it could happen:
aaabbbbb
another way it could happen would be:
aababbbb
another way it could happen would be:
aabbabbb
etc.
so the probability you calculated is correct but for only one of the ways it could happen.
there were 55 other ways it could happen as well.

the binomial probability formula takes that into account.
p(x) = nCx * p^x * q^(*n-x)
nCx is the number of possible ways to get x things from n.
p = probability of the event occurring.
q k= probability of the event not occurring = 1 - p.