SOLUTION: Find all values of t in the interval [0, 2π] satisfying the given equation. 2 sin 2t-(sqrt 6) tan 2t = 0

Since we want t to be in the interval [0,] we have to
find all values of 2t in [0,] and interval.  That's because

since 

then

      



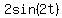
Substitute 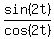 for 



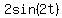
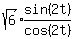
Multiply through by cos(2t) which we must require that
cos(2t) NOT EQUAL ZERO! because if it were zero we'd be
multiplying both sides of an equation by zero which is
not a valid operation.

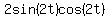
 with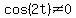 

Factor out sin(2t) 



Use the zero-factor principle:

;  

Taking the first equation

sin(2t) = 0

2t = 0,,,,

so divide them all by 2 to solve for the values of t

t = 0,,,,.

So there are 5 solutions in the interval [0,].
And there may be more from the second equation.  

Taking the second equation:







But 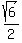 is more than 1, in fact it's like 1.224744871

and no cosine can ever exceed 1 (except in much higher mathematics
courses, but forget that for now).

So there were no additional solutions from the
second equation.

So the only possible solutions are:

t = 0,,,,.

We must also check to see if any are extraneous solutions 
because we multiplied through by  and had to 
require tha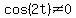t ,

But  is either 1 or -1 for each of those, never
0.  So 

t = 0,,,,.

are the only solutions in [0,]

Edwin